题目内容
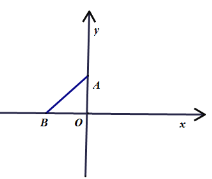
【题目】如图,在直角坐标平面内有两点![]() 、
、![]() ,且
,且![]() 、
、![]() 两点之间的距离等于
两点之间的距离等于![]() (
(![]() 为大于0的已知数),在不计算
为大于0的已知数),在不计算![]() 的数值条件下,完成下列两题:
的数值条件下,完成下列两题:
(1)以学过的知识用一句话说出![]() 的理由;
的理由;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形,如果存在,请写出点
是等腰三角形,如果存在,请写出点![]() 的坐标,并求
的坐标,并求![]() 的面积;如果不存在,请说明理由.
的面积;如果不存在,请说明理由.
【答案】(1)垂线段最短;(2)存在,当![]() ,
,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() .
.
【解析】
(1)利用垂线段最短即可得出结论;
(2)分类讨论,利用等腰三角形的判定可得出P点坐标,利用三角形面积公式得出结论.
解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,
∵![]() ,
,
∴![]() ,
,
∵垂线段最短,且![]() 不与O重合,
不与O重合,
∴![]() ,即
,即![]() ,
,
∴![]() 的理由是“垂线段最短”;
的理由是“垂线段最短”;
(2)在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
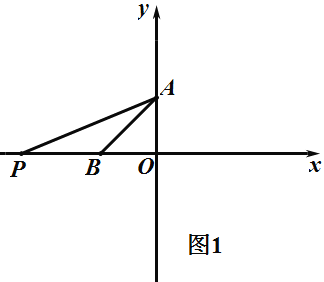
①如图1,当P在B点左边,BP=BA=a,![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
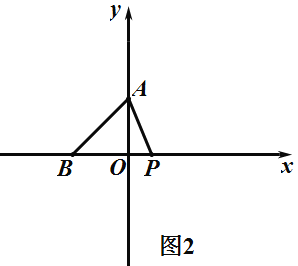
②如图2,当P在B点右边,BP=BA=a,![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
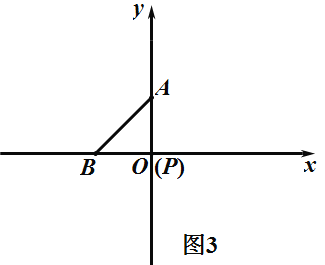
③如图3,当P在B点右边,BP=AP,![]() 为等腰三角形,
为等腰三角形,
此时P与O重合,即![]() ,
,
∵![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
④如图4,当P在B点右边,AP=AB=a,![]() 为等腰三角形,
为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;

综上所述:在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;

练习册系列答案
相关题目