题目内容
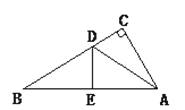
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 . 
【答案】![]() +
+ ![]()
【解析】解:如图,连接AD,
由题意得:CA=CD,∠ACD=60°,
∴△ACD为等边三角形,
∴AD=CA,∠DAC=∠DCA=∠ADC=60°;
∵∠ABC=90°,AB=BC=2,
∴AC=AD=2 ![]() ,
,
∵AC=AD,CE=ED,
∴AE垂直平分DC,
∴EO= ![]() DC=
DC= ![]() ,OA=CAsin60°=
,OA=CAsin60°= ![]() ,
,
∴AE=EO+OA= ![]() +
+ ![]() ,
,
故答案为 ![]() +
+ ![]() .
.
如图,连接AD,由题意得:CA=CD,∠ACD=60°,得到△ACD为等边三角形根据AC=AD,CE=ED,得出AE垂直平分DC,于是求出EO= ![]() DC=
DC= ![]() ,OA=ACsin60°=
,OA=ACsin60°= ![]() ,最终得到答案AE=EO+OA=
,最终得到答案AE=EO+OA= ![]() +
+ ![]() .本题考查了图形的变换﹣旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.
.本题考查了图形的变换﹣旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.

练习册系列答案
相关题目