题目内容
 如图,小明同学在夜晚由路灯AB走向路灯CD,当他走到点E时,发现身后他头顶部F的影子刚好接触到路灯AB的底部A处,当他向前再步行18m到达G点时,发现身前他头顶部H的影子刚好接触到路灯CD的底部C处,已知小明同学的身高是1.6m,两个路灯的高度相等,两个路灯之间的距离AC=30m.则路灯的高度是________ m.
如图,小明同学在夜晚由路灯AB走向路灯CD,当他走到点E时,发现身后他头顶部F的影子刚好接触到路灯AB的底部A处,当他向前再步行18m到达G点时,发现身前他头顶部H的影子刚好接触到路灯CD的底部C处,已知小明同学的身高是1.6m,两个路灯的高度相等,两个路灯之间的距离AC=30m.则路灯的高度是________ m.
8
分析:根据平行线得出比例式,求出AE=CG,再求出AE、CG的值,最后根据比例式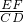 =
= ,求出AB即可.
,求出AB即可.
解答:∵EF∥CD,GH∥AB,
∴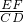 =
= ,
, =
= ,
,
∴AE= ,CG=
,CG= ,
,
∵EF=GH,AB=CD,
∴AE=CG,
即AE=CG= (AC-EG)=
(AC-EG)= ×(30-18)=6,
×(30-18)=6,
∵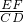 =
= ,
,
∴ =
= ,
,
∴CD=8,
故答案为:8.
点评:本题考查了平行线分线段成比例定理和相似三角形的性质和判定等知识点,解此题的关键是求出AE、CG的长,借助一个等式 =
= )推出AE=CG.题型较好,用的数学思想是转化思想,即把实际问题转化成数学问题.
)推出AE=CG.题型较好,用的数学思想是转化思想,即把实际问题转化成数学问题.
分析:根据平行线得出比例式,求出AE=CG,再求出AE、CG的值,最后根据比例式
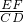 =
= ,求出AB即可.
,求出AB即可.解答:∵EF∥CD,GH∥AB,
∴
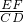 =
= ,
, =
= ,
,∴AE=
 ,CG=
,CG= ,
,∵EF=GH,AB=CD,
∴AE=CG,
即AE=CG=
 (AC-EG)=
(AC-EG)= ×(30-18)=6,
×(30-18)=6,∵
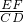 =
= ,
,∴
 =
= ,
,∴CD=8,
故答案为:8.
点评:本题考查了平行线分线段成比例定理和相似三角形的性质和判定等知识点,解此题的关键是求出AE、CG的长,借助一个等式
 =
= )推出AE=CG.题型较好,用的数学思想是转化思想,即把实际问题转化成数学问题.
)推出AE=CG.题型较好,用的数学思想是转化思想,即把实际问题转化成数学问题. 
练习册系列答案
相关题目
 如图,小明同学在夜晚由路灯AB走向路灯CD,当他走到点E时,发现身后他头顶部F的影子刚好接触到路灯AB的底部A处,当他向前再步行18m到达G点时,发现身前他头顶部H的影子刚好接触到路灯CD的底部C处,已知小明同学的身高是1.6m,两个路灯的高度相等,两个路灯之间的距离AC=30m.则路灯的高度是
如图,小明同学在夜晚由路灯AB走向路灯CD,当他走到点E时,发现身后他头顶部F的影子刚好接触到路灯AB的底部A处,当他向前再步行18m到达G点时,发现身前他头顶部H的影子刚好接触到路灯CD的底部C处,已知小明同学的身高是1.6m,两个路灯的高度相等,两个路灯之间的距离AC=30m.则路灯的高度是