Question

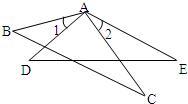
如图，已知AB⊥AD，CD⊥AD，∠1=∠2，完成下列推理过程：
证明：∵AB⊥AD，CD⊥AD（已知）
∴________=________=90°（ 垂直定义 ）
又∵∠1=∠2 （ 已知 ）
∴∠BAD-∠1=∠CDA-________
即∠DAE=∠ADF
∴DF∥________（________）

Answer 1

∠DAB    ∠CDA    ∠2    AE    内错角相等，两直线平行
分析：由垂直得出直角：∠DAB=∠CDA=90°；然后利用等量代换求得内错角∠DAE=∠ADF，已知两直线DF、AE相互平形．
解答：证明：∵AB⊥AD，CD⊥AD（已知），
∴∠DAB=∠CDA=90°（ 垂直定义 ）．
又∵∠1=∠2 （ 已知 ），
∴∠BAD-∠1=∠CDA-∠2，即∠DAE=∠ADF，
∴DF∥AE（内错角相等，两直线平行）．
故答案分别是：∠DAB，∠CDA；∠2；AE，内错角相等，两直线平行．
点评：本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．