题目内容
如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.
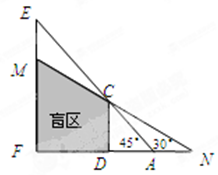

A、N之间的距离为( )米.
)米.
 )米.
)米.试题分析:主要利用解直角三角形,求出AN的长度即可.
试题解析:由题意可知:∠CDA=90°;
在Rt△CAD中,∠CDA=90°,∠CAD=45°,CD=15,
∴
 .
.在Rt△CDN中,∠CDN=90°,∠CND=30°,
∴
 .
.∴
 (米).
(米).故A、N之间的距离为(
 )米.
)米.考点:特殊角的三角函数值.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
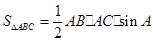 ;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,
;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,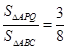 ?
?
 ,则BD的长为 。
,则BD的长为 。




 ,则β的取值范围为( )
,则β的取值范围为( ) .
. .
. 分别是
分别是 的三个内角,若
的三个内角,若 ,则
,则 ,那么∠A=( )
,那么∠A=( )



