题目内容
如图：在⊙O中∠A=25°，∠E=30°，∠BOD的度数为________．
110°
分析：连接OC，利用同弧所对的圆心角等于所对圆周角的2倍，得到∠BOC=2∠A，∠COD=2∠E，由∠A与∠E的度数即可求出∠BOD的度数．
解答：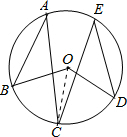
解：连接OC，
∵∠A与∠BOC都对
，∠E与∠COD都对
，
∴∠BOC=2∠A，∠COD=2∠E，
∵∠A=25°，∠E=30°，
∴∠BOD=∠BOC+∠COD=50°+60°=110°．
故答案为：110°
点评：此题考查了圆周角定理，熟练掌握圆周角定理是解本题的关键．
分析：连接OC，利用同弧所对的圆心角等于所对圆周角的2倍，得到∠BOC=2∠A，∠COD=2∠E，由∠A与∠E的度数即可求出∠BOD的度数．
解答：
解：连接OC，∵∠A与∠BOC都对
，∠E与∠COD都对，∴∠BOC=2∠A，∠COD=2∠E，
∵∠A=25°，∠E=30°，
∴∠BOD=∠BOC+∠COD=50°+60°=110°．
故答案为：110°
点评：此题考查了圆周角定理，熟练掌握圆周角定理是解本题的关键．
练习册系列答案
天天向上口算本系列答案
相关题目
19、如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，试说明∠1=∠2，以下是证明过程，请填空：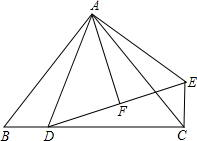
如图，在△ABC中，已知AB=AC，∠BAC=90°，D是BC上一点，EC⊥BC，EC=BD，DF=FE．求证：
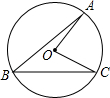如图，在⊙O中，∠ABC=40°，则∠AOC=
如图，在△ABC中，∠B，∠C的外角平分线相交于点O，若∠A=74°，则∠O=
15、如图，在△ABC中，AQ=PQ，PR=PS，PS⊥AC于S，PR⊥AB于R，则以下结论中：（1）AS=AR；（2）△BRP∽△QSP；（3）PQ∥AB中，正确的有