题目内容
如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD
的内心. 求证:(1)OI是△IBD的外接圆的切线;(2)AB+AD=2BD.

解:(1)如图,根据三角形内心的性质和同弧上圆周角的性质知
![]() ,
,![]() .
.
 所以
所以![]() , CI = CD.
, CI = CD.
同理,CI = CB .故点C是△IBD的外心.连接OA,OC,因为I是AC的中点,
且OA = OC,所以OI⊥AC,即OI⊥CI .故OI是△IBD外接圆的切线.
(2)如图,过点I作IE⊥AD于点E,设OC与BD交于点F.
由![]() ,知OC⊥BD.
,知OC⊥BD.
因为∠CBF =∠IAE,BC = CI = AI,所以![]() .所以BF = AE.
.所以BF = AE.
又因为I是△ABD的内心,所以![]() .
.
故![]() .
.

练习册系列答案
相关题目
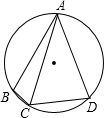 如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为( )
如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
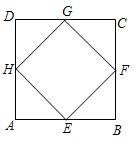
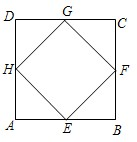 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4. 如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为
如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为


 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.