Question

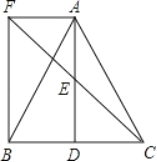
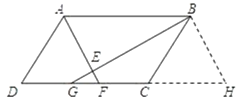
【题目】如图，在平行四边形 中，、 的平分线 分别与线段 交于点 ， 与 交于点 ．

(1) 求证：，；

(2) 若 ，，，求 和 的长度．

Answer 1

【答案】(1)证明见解析；(2) 的长度为 2，的长度为 ．

【解析】

（1）由在平行四边形 中，、 的平分线 分别与线段交于点 ，易求得 ，即可得，证得 ，易证得与 是等腰三角形，即可得 ，，又由 ，即可证得；

（2）由（1）易求得 ，，即可求得 的长；过点 作 交 的延长线于点 ，易证得四边形 为平行四边形，即可得是直角三角形，然后利用勾股定理，即可求得 的长．

(1) 证明：∵ 平分，

∴．

∵平分，

∴．

∵ 四边形 平行四边形，

∴，，，

∴，

∴．

∴．

∴；

∵，

∴，

∴，

∴，

∵，

∴，

∴，

∴，

∵．

∴；

(2) 解：∵，

∴．

∴，

∵四边形 平行四边形，

∴．

∴，

∴，

过点 作 交 的延长线于点 ．

∴．

∵，

∴四边形 为平行四边形．

∴，．

∴，

∴在 中：．

∴ 的长度为 2，的长度为 ．

故答案为：(1)证明见解析；(2) 的长度为 2，的长度为 ．