题目内容
 如图,D、E分别为△ABC的边AB、AC的中点,CD、BE相交于O,S△ODE=a,则S△ABC等于
如图,D、E分别为△ABC的边AB、AC的中点,CD、BE相交于O,S△ODE=a,则S△ABC等于
- A.8a
- B.10a
- C.12a
- D.6a
C
分析:首先由三角形的中位线判断:DE∥BC,DE= BC,则可证得:△ODE∽△OCB,△ADE∽△ABC;又由相似三角形的面积比等于相似比的平方,可求得S△OBC的值,根据等高三角形的面积比等于对应底的比,可得S△ODB=S△OEC=2a,即可求得S△ABC的值.
BC,则可证得:△ODE∽△OCB,△ADE∽△ABC;又由相似三角形的面积比等于相似比的平方,可求得S△OBC的值,根据等高三角形的面积比等于对应底的比,可得S△ODB=S△OEC=2a,即可求得S△ABC的值.
解答:∵D、E分别为△ABC的边AB、AC的中点,
∴DE∥BC,DE= BC,
BC,
∴△ODE∽△OCB,△ADE∽△ABC,
∴ ,
, ,
,
∵S△ODE=a,
∴S△OBC=4a,S△ODB=S△OEC=2a,
∴S梯形DBCE=S△ODE+S△OBC+S△ODB+S△OEC=9a,
∴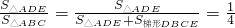 ,
,
∴S△ADE=3a,
∴S△ABC=12a.
故选C.
点评:此题考查了相似三角形的判定与性质,以及三角形中位线的性质等知识.注意相似三角形的面积比等于相似比的平方,等高三角形的面积比等于底的比.
分析:首先由三角形的中位线判断:DE∥BC,DE=
 BC,则可证得:△ODE∽△OCB,△ADE∽△ABC;又由相似三角形的面积比等于相似比的平方,可求得S△OBC的值,根据等高三角形的面积比等于对应底的比,可得S△ODB=S△OEC=2a,即可求得S△ABC的值.
BC,则可证得:△ODE∽△OCB,△ADE∽△ABC;又由相似三角形的面积比等于相似比的平方,可求得S△OBC的值,根据等高三角形的面积比等于对应底的比,可得S△ODB=S△OEC=2a,即可求得S△ABC的值.解答:∵D、E分别为△ABC的边AB、AC的中点,
∴DE∥BC,DE=
 BC,
BC,∴△ODE∽△OCB,△ADE∽△ABC,
∴
 ,
, ,
,∵S△ODE=a,
∴S△OBC=4a,S△ODB=S△OEC=2a,
∴S梯形DBCE=S△ODE+S△OBC+S△ODB+S△OEC=9a,
∴
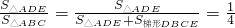 ,
,∴S△ADE=3a,
∴S△ABC=12a.
故选C.
点评:此题考查了相似三角形的判定与性质,以及三角形中位线的性质等知识.注意相似三角形的面积比等于相似比的平方,等高三角形的面积比等于底的比.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
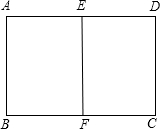 如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD
如图,E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD 5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )
5、如图,A、B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )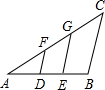 如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF=
如图,D,E分别为AB的三等分点,DF∥EG∥BC,若BC=12,则DF=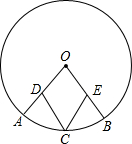 如图,D、E分别为⊙O半径OA、OB的中点,C是
如图,D、E分别为⊙O半径OA、OB的中点,C是
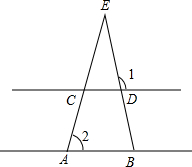 (2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )
(2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )