题目内容
⊙O中AB是直径，AC是弦，点B，C间的距离是2cm，那么圆心到弦AC的距离是________cm．
1
分析：先画出图形，由圆周角定理得∠C=90°，则OD∥BC，再由三角形的中位线定理，得OD=
BC=1cm．
解答：
解：如图，
∵AB是直径，∴∠C=90°，
∵OD⊥AC，∴OD∥BC，
∴OD=BC，
∵BC=2cm，
∴OD=1cm，
∴圆心到弦AC的距离是1cm，
故答案为1．
点评：本题考查了垂径定理和勾股定理，解此类题目要注意将圆的问题转化成三角形的问题再进行计算．
分析：先画出图形，由圆周角定理得∠C=90°，则OD∥BC，再由三角形的中位线定理，得OD=
BC=1cm．解答：
解：如图，∵AB是直径，∴∠C=90°，
∵OD⊥AC，∴OD∥BC，
∴OD=
BC，∵BC=2cm，
∴OD=1cm，
∴圆心到弦AC的距离是1cm，
故答案为1．
点评：本题考查了垂径定理和勾股定理，解此类题目要注意将圆的问题转化成三角形的问题再进行计算．
练习册系列答案
相关题目
不是，说明理由．
如图，在圆O中AB是直径，AT是经过点A的切线，弦CD垂直AB于P点，线段CP的中点为Q，连接BQ并延长交切线AT于T点，连接OT．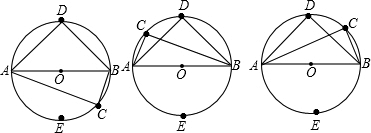
说明理由；若不成立，请用含m、n的式子表示tan∠DAC．（直接写答案）
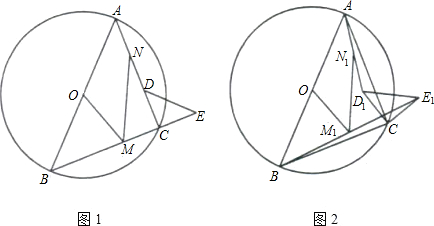
如图甲，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角△DCE中，∠DCE是直角，点D在线段AC上．