题目内容
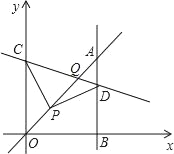
【题目】如图，平面直角坐标系中，已知直线y=x上一点P（2，2），C为y轴上一点，连接PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线y=x交于点A，连接CD，直线CD与直线y=x交于点Q，当△OPC≌△ADP时，则C点的坐标是_____，Q点的坐标是_____．
【答案】（0，4+2
）（2+2，2+2）
【解析】
过P点作x轴的平行线交y轴于M，交AB于N，如图，设C（0，t），OP=2，OM=BN=PM=2，CM=t﹣2，利用旋转性质得PC=PD，∠CPD=90°，再证明△PCM≌△DPN得到PN=CM=t﹣2，DN=PM=2，于是得到D（t，4），接着利用△OPC≌△ADP得到AD=OP=2，则A（t，4+2），于是利用y=x图象上点的坐标特征得到t=4+2，所以C（0，4+2），D（4+2，4），接下来利用待定系数求出直线CD的解析式为y=（1﹣）x+4+2，则通过解方程组
可得Q点坐标．
过P点作x轴的平行线交y轴于M，交AB于N，如图，设C（0，t），∴P（2，2），∴OP=2，OM=BN=PM=2，CM=t﹣2．
∵线段PC绕点P顺时针旋转90°至线段PD，∴PC=PD，∠CPD=90°，∴∠CPM+∠DPN=90°，
而∠CPM+∠PCM=90°，∴∠PCM=∠DPN，
在△PCM和△DPN中，∵
，∴△PCM≌△DPN，∴PN=CM=t﹣2，DN=PM=2，∴MN=t﹣2+2=t，DB=2+2=4，∴D（t，4）．
∵△OPC≌△ADP，∴AD=OP=2，∴A（t，4+2），
把A（t，4+2）代入y=x得：t=4+2，∴C（0，4+2），D（4+2，4），
设直线CD的解析式为y=kx+b，
把C（0，4+2），D（4+2，4）代入得：
，解得：
，∴直线CD的解析式为y=（1﹣）x+4+2，
解方程组，得：
，∴Q（2+2，2+2）．
故答案为：（0，4+2），（2+2，2+2）．
