题目内容
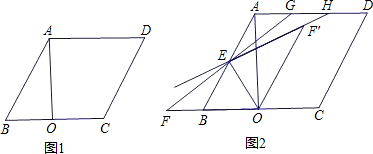
如图1,在□ABCD中,∠BCD的平分线交直线AD于点F,∠BAD的平分线交DC延长线于E.(1)在图1中,证明AF=EC;

(2)若∠BAD=90°,G为CF的中点(如图2),判断△BEG的形状,并证明.
⑴略⑵等腰直角三角形,理由:略
解析:⑴通过已知,可得△ADE, △FDC为等腰三角形,从而得出结论
⑵因为已知∠BAD=90°,G为CF的中点,则作辅助线,GH,HT,分别垂直于直线BC,CD,垂足为H,T,那么利用三角形的全等可知,BG=EG,然后利用直角三角形BCW,可以解得BE= ,从而得到△BEG的形状为等腰直角三角形。
,从而得到△BEG的形状为等腰直角三角形。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
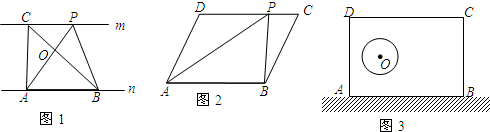



 )时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
)时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.