Question

如图，抛物线y=-

1

2

x2+

3

2

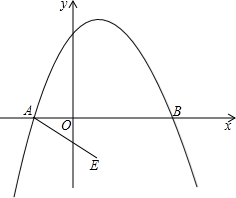x+2与x轴的交于A，B两点．点E（1，-1），以A、E为顶点作平行四边形AEMN，使点M，N都在抛物线上．求点M，N的坐标．

Answer 1

分析：主要考查抛物线的有关性质，可得A点坐标，由A、E之间关系和平行四边形性质得出M、N两点的关系，代入抛物线方程，求出M、N两点坐标．

解答：解：由-

1

2

x2+

3

2

x+2=0得A（-1，0）
点E向上平移1个单位，再向左平移2个单位后与点A重合，
∵AEMN是平行四边形
∴点M与点E作同样的平移后与点N重合
设M（a，b），则N（a-2，b+1）
∵点M，N都在抛物线y=-

1

2

x2+

3

2

x+2
∴-

1

2

a2+

3

2

a+2=b①
-

1

2

(a+1)2+

3

2

(a+1)+2=b-2②
由①②可解得a=3 b=2
则M（3，2），N（1，3）．

点评：本题综合考查了抛物线、坐标点的移动及平行四边形的性质，很适合学生进行练习，是一道不可多得的综合性试题．