题目内容
如图所示，圆柱体ABCD中，AB=3，AD=4π，现用一根绳子从A点绕圆柱体一周连接到D点，则这根绳子的最短长度为5π
5π
．分析：要求这根绳子的最短长度，需将圆柱的侧面展开，进而根据勾股定理得出结果．
解答：
解：如图，将圆柱体展开，得到矩形ADD′A′，连接AD′，则线段AD′的长即为绳子最短的长度．
在△ADD′中，DD′=3π，AD=4π，
由勾股定理，得AD′=
=5π，
即这根绳子的最短长度为5π．
故答案为5π．
解：如图，将圆柱体展开，得到矩形ADD′A′，连接AD′，则线段AD′的长即为绳子最短的长度．在△ADD′中，DD′=3π，AD=4π，
由勾股定理，得AD′=
| AD2+DD′2 |
即这根绳子的最短长度为5π．
故答案为5π．
点评：本题考查了平面展开-最短路径问题及圆柱体的侧面展开图，掌握圆柱体的侧面展开图是一个矩形，其中矩形的长是圆柱的底面周长，宽是圆柱的高是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，是一个圆柱体，ABCD是它的一个横截面，AB=| 8 |
| π |
| A、7 | ||||
B、
| ||||
C、
| ||||
| D、5 |
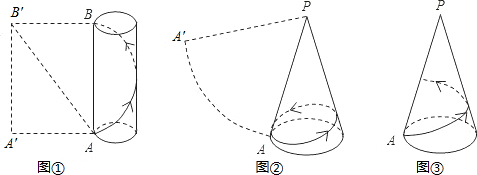
如图所示，圆柱体ABCD中，AB=3，AD=4π，现用一根绳子从A点绕圆柱体一周连接到D点，则这根绳子的最短长度为________．