题目内容
 如图,直线l经过点A(-3,1)、B(0,-2),将该直线向右平移2个单位得到直线l′.
如图,直线l经过点A(-3,1)、B(0,-2),将该直线向右平移2个单位得到直线l′.(1)在图中画出直线l′的图象;
(2)求直线l′的解析式.
分析:(1)过(-1,1),(2,-2),两点即可.
(2)用待定系数法求得原函数解析式.
(2)用待定系数法求得原函数解析式.
解答: 解:(1)如图.
解:(1)如图.
(2)图象特征:过原点且与l平行(如图)(3分)
点A向右平移两个单位后坐标为(-1,1),点B向右平移两个单位后坐标这(2,-2),即直线l′经过点(-1,1)和(2,-2).(5分)
设直线l′的解析式为y=kx+b(k≠0)
所以
,(7分)
解这个方程组,得k=-1,b=0
∴直线l′的解析式为y=-x.(9分)
 解:(1)如图.
解:(1)如图.(2)图象特征:过原点且与l平行(如图)(3分)
点A向右平移两个单位后坐标为(-1,1),点B向右平移两个单位后坐标这(2,-2),即直线l′经过点(-1,1)和(2,-2).(5分)
设直线l′的解析式为y=kx+b(k≠0)
所以
|
解这个方程组,得k=-1,b=0
∴直线l′的解析式为y=-x.(9分)
点评:求解析式通常用待定系数法;注意平移时k的值不变,只有b发生变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
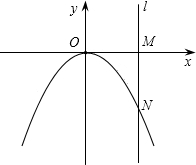 如图,直线l经过点M(3,0),且平行于y轴,与抛物线y=ax2交于点N,若S△OMN=9,则a的值是( )
如图,直线l经过点M(3,0),且平行于y轴,与抛物线y=ax2交于点N,若S△OMN=9,则a的值是( )A、
| ||
B、-
| ||
C、
| ||
D、-
|
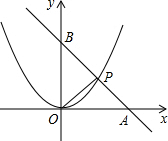 如图,直线l经过点A(4,0)和点B(0,4),且与二次函数y=ax2的图象在第一象限内相交于点P,若△AOP的面积为
如图,直线l经过点A(4,0)和点B(0,4),且与二次函数y=ax2的图象在第一象限内相交于点P,若△AOP的面积为 (2013•赤峰)如图,直线L经过点A(0,-1),且与双曲线c:y=
(2013•赤峰)如图,直线L经过点A(0,-1),且与双曲线c:y= (2012•天河区一模)如图,直线l经过点A(1,0),且与曲线
(2012•天河区一模)如图,直线l经过点A(1,0),且与曲线