题目内容
一元二次方程x2+kx+3=0没有实数根，则k满足的条件是
- A.k2＞12
- B.k2≥12
- C.k2＜12
- D.k2≤12
C
分析：根据方程没有实数根得到其根的判别式小于0，据此可以得到关于k的不等式．
解答：∵一元二次方程x2+kx+3=0没有实数根，
∴△=k2-3×4＜0，
即：k2＜12
故选C．
点评：本题考查了根的判别式，当一元二次方程没有实数根时，根的判别式小于零．
分析：根据方程没有实数根得到其根的判别式小于0，据此可以得到关于k的不等式．
解答：∵一元二次方程x2+kx+3=0没有实数根，
∴△=k2-3×4＜0，
即：k2＜12
故选C．
点评：本题考查了根的判别式，当一元二次方程没有实数根时，根的判别式小于零．
练习册系列答案
相关题目
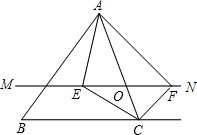从甲、乙两题中选做一题，如果两题都做，只以甲题计分．