题目内容
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,S△ABC=8![]() ,点M,P,N分别是边AB,BC,AC上任意一点,则:
,点M,P,N分别是边AB,BC,AC上任意一点,则:
(1)AB的长为____________.
(2)PM+PN的最小值为____________.

【答案】4![]() ; 2
; 2![]() .
.
【解析】
![]() 过点A作
过点A作![]() ,垂足为G,依据等腰三角形的性质可得到
,垂足为G,依据等腰三角形的性质可得到![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,然后依据三角形的面积公式列方程求解即可;
,然后依据三角形的面积公式列方程求解即可;
![]() 作点A关于BC的对称点
作点A关于BC的对称点![]() ,取
,取![]() ,则
,则![]() ,过点
,过点![]() 作
作![]() ,垂足为D,当
,垂足为D,当![]() 、P、M在一条直线上且
、P、M在一条直线上且![]() 时,
时,![]() 有最小值,其最小值
有最小值,其最小值![]() .
.
(1)如图所示:过点A作AG⊥BC,垂足为G,
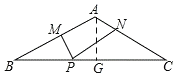
∵AB=AC,∠BAC=120°,∴∠ABC=30°,
设AB=x,则AG![]() ,BG
,BG![]() x,则BC
x,则BC![]() x,
x,
∴![]() BCAG
BCAG![]()
![]() x
x![]() x=8
x=8![]() ,解得:x=4
,解得:x=4![]() ,∴AB的长为4
,∴AB的长为4![]() ,
,
故答案为:4![]() ;
;
(2)如图所示:作点A关于BC的对称点A',取CN=CN',则PN=PN',过点A'作A'D⊥AB,垂足为D,
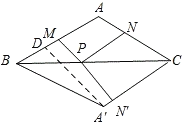
当N'、P、M在一条直线上且MN'⊥AB时,PN+PM有最小值,
最小值=MN'=DA'![]() AB=2
AB=2![]() ,
,
故答案为:2![]() .
.

练习册系列答案
相关题目