题目内容
 在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
解:在Rt△BCD中,
∵∠BCD=90°-30°=60°,
∴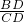 =tan60°,则BD=
=tan60°,则BD= CD.
CD.
在Rt△ABD中,∵∠ABD=60°,
∴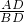 =tan60°,即
=tan60°,即 =
= ,
,
解得:CD=20,
∴BD= CD=20
CD=20 ≈35.
≈35.
分析:在直角三角形BCD中,求出∠BCD的度数,利用锐角三角形函数定义表示出tan∠BCD,得到BD与CD的关系,在直角三角形ABD中,由∠ABD的度数,利用锐角三角形函数定义表示出tan∠ABD,将AD=AC+CD,及用CD表示出的BD代入列出关于CD的方程,求出方程的解得到CD的长,进而确定出BD的长,取近似值即可得到结果.
点评:此题考查了解直角三角形的应用-仰角俯角问题,涉及的知识有:锐角三角函数定义,特殊角的三角函数值,利用了转化的思想,是一道中档题.
∵∠BCD=90°-30°=60°,
∴
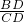 =tan60°,则BD=
=tan60°,则BD= CD.
CD.在Rt△ABD中,∵∠ABD=60°,
∴
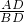 =tan60°,即
=tan60°,即 =
= ,
,解得:CD=20,
∴BD=
 CD=20
CD=20 ≈35.
≈35.分析:在直角三角形BCD中,求出∠BCD的度数,利用锐角三角形函数定义表示出tan∠BCD,得到BD与CD的关系,在直角三角形ABD中,由∠ABD的度数,利用锐角三角形函数定义表示出tan∠ABD,将AD=AC+CD,及用CD表示出的BD代入列出关于CD的方程,求出方程的解得到CD的长,进而确定出BD的长,取近似值即可得到结果.
点评:此题考查了解直角三角形的应用-仰角俯角问题,涉及的知识有:锐角三角函数定义,特殊角的三角函数值,利用了转化的思想,是一道中档题.

练习册系列答案
相关题目
 已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米)
已知:如图,初二•一班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC.(精确到0.1米) 在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)
在建筑物顶部A处测得B处的俯角为60°,在C处测得B处的俯角为30°,已知AC=40米,求BD之间的直线距离.(结果精确到个位)

