题目内容
 如图是一个高为
如图是一个高为 cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是
cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是
- A.4cm
- B.(
 )cm
)cm - C.
 cm
cm - D.(
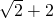 )cm
)cm
B
分析:易求得圆锥的底面周长,利用勾股定理易得圆锥的母线长,那么可求得扇形的圆心角,所以圆形纸片的最大半径为应为和扇形相切的圆的半径.
解答: 解:∵圆锥的高为2
解:∵圆锥的高为2 cm,底面半径为2cm,
cm,底面半径为2cm,
∴圆锥的母线长为 =8cm;圆锥的底面周长为4πcm,
=8cm;圆锥的底面周长为4πcm,
设扇形的圆心角为n,
∴ =4π,
=4π,
解得n=90°,
设圆形纸片的半径为OB=x.
∴OA= =
= x,
x,
∴x+ x=8,
x=8,
解得:x=8 -8,
-8,
这个圆形纸片的半径最长可以是8 -8cm.
-8cm.
故选:B.
点评:此题主要考查了圆锥的计算,用到的知识点为:圆锥的高,母线长,底面半径组成直角三角形;圆锥的侧面展开图的弧长等于底面周长.
分析:易求得圆锥的底面周长,利用勾股定理易得圆锥的母线长,那么可求得扇形的圆心角,所以圆形纸片的最大半径为应为和扇形相切的圆的半径.
解答:
 解:∵圆锥的高为2
解:∵圆锥的高为2 cm,底面半径为2cm,
cm,底面半径为2cm,∴圆锥的母线长为
 =8cm;圆锥的底面周长为4πcm,
=8cm;圆锥的底面周长为4πcm,设扇形的圆心角为n,
∴
 =4π,
=4π,解得n=90°,
设圆形纸片的半径为OB=x.
∴OA=
 =
= x,
x,∴x+
 x=8,
x=8,解得:x=8
 -8,
-8,这个圆形纸片的半径最长可以是8
 -8cm.
-8cm.故选:B.
点评:此题主要考查了圆锥的计算,用到的知识点为:圆锥的高,母线长,底面半径组成直角三角形;圆锥的侧面展开图的弧长等于底面周长.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( )
cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( ) 4,
4, 2)
2)
 cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( )
cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( )
 )cm
)cm cm
cm )cm
)cm cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( )
cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( ) 4,
4, 2)
2)
 cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( )
cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( ) 4,
4, 2)
2)
 cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( )
cm,底面半径为2cm的圆锥形无底纸帽,现利用这个纸帽的侧面纸张裁剪出一个圆形纸片(不考虑纸帽接缝),这个圆形纸片的半径最长可以是( ) 4,
4, 2)
2)