题目内容
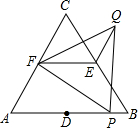 (2013•贵港)如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE=
(2013•贵港)如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE=2
2
.分析:连结FD,根据等边三角形的性质由△ABC为等边三角形得到AC=AB=6,∠A=60°,再根据点D、E、F分别是等边△ABC三边的中点,则AD=BD=AF=3,DP=2,EF为△ABC的中位线,于是可判断△ADF为等边三角形,得到∠FDA=60°,利用三角形中位线的性质得EF∥AB,EF=
AB=3,根据平行线性质得∠1+∠3=60°;又由于△PQF为等边三角形,则∠2+∠3=60°,FP=FQ,所以∠1=∠2,然后根据“SAS”判断△FDP≌△FEQ,所以DP=QE=2.
| 1 |
| 2 |
解答:解:连结FD,如图 ,
,
∵△ABC为等边三角形,
∴AC=AB=6,∠A=60°,
∵点D、E、F分别是等边△ABC三边的中点,AB=6,PB=1,
∴AD=BD=AF=3,DP=DB-PB=3-1=2,EF为△ABC的中位线,
∴EF∥AB,EF=
AB=3,△ADF为等边三角形,
∴∠FDA=60°,
∴∠1+∠3=60°,
∵△PQF为等边三角形,
∴∠2+∠3=60°,FP=FQ,
∴∠1=∠2,
∵在△FDP和△FEQ中
,
∴△FDP≌△FEQ(SAS),
∴DP=QE,
∵DP=2,
∴QE=2.
故答案为2.
 ,
,∵△ABC为等边三角形,
∴AC=AB=6,∠A=60°,
∵点D、E、F分别是等边△ABC三边的中点,AB=6,PB=1,
∴AD=BD=AF=3,DP=DB-PB=3-1=2,EF为△ABC的中位线,
∴EF∥AB,EF=
| 1 |
| 2 |
∴∠FDA=60°,
∴∠1+∠3=60°,
∵△PQF为等边三角形,
∴∠2+∠3=60°,FP=FQ,
∴∠1=∠2,
∵在△FDP和△FEQ中
|
∴△FDP≌△FEQ(SAS),
∴DP=QE,
∵DP=2,
∴QE=2.
故答案为2.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 (2013•贵港)如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
(2013•贵港)如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( ) (2013•贵港)如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=
(2013•贵港)如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ= (2013•贵港)如图,点A(a,1)、B(-1,b)都在双曲线y=-
(2013•贵港)如图,点A(a,1)、B(-1,b)都在双曲线y=- (2013•贵港)如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )
(2013•贵港)如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( ) (2013•贵港)如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2
(2013•贵港)如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2