题目内容
已知:正方形ABCD的边长为2,⊙O交正方形ABCD的对角线AC所在直线于点T,连结TO交⊙O于点S,连结AS.

1.如图1,当⊙O经过A、D两点且圆心O在正方形ABCD内部时,连结DT、DS.
①试判断线段DT、DS的数量关系和位置关系; ②求AS+AT的值;
2.如图2,当⊙O经过A、D两点且圆心O在正方形ABCD外部时,连结DT、DS.求AS-AT的值;
3.如图3,延长DA到点E,使AE=AD,当⊙O经过A、E两点时,连结ET、ES.
根据(1)、(2)计算,通过观察、分析,对线段AS、AT的数量关系提出问题并解答.
1.①线段DT、DS的数量和位置关系分别是DT=DS和DT⊥DS…2分
………3分
②证△DAS≌△DCT ……4分
∴AS+AT=![]() …………5分
…………5分
2.证△DAS≌△DCT …………6分
∴AS-AT=![]() …………8分
…………8分
3.提出的问题是:求 AT-AS 的值. …………10分
在TA上取TF=AS,连结EF,证△EAS≌△EFT …………11分
∴ AT-AS =![]() …………12分
…………12分
解析:(1)因为ST是直径,所以![]() °,AC是正方形的对角线,所以也是角平分线,从而三角形SDT是等腰直角三角形;由△DAS≌△DCT,可知AS=CT,这样就把AS+AT转化为CT+AT,易得CT+AT=
°,AC是正方形的对角线,所以也是角平分线,从而三角形SDT是等腰直角三角形;由△DAS≌△DCT,可知AS=CT,这样就把AS+AT转化为CT+AT,易得CT+AT=![]() ;
;
(2)(3)小题都是以(1)题为基础,解题思路相同

 如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )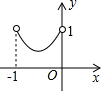
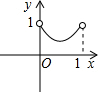
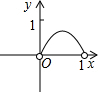
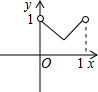
 由.
由. s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒.
s的速度运动,同时动点Q在线段FC上从F?C以1cm/s的速度运动,动点G在PC上,且∠EGC=∠EQC,连接PD.设运动时间为t秒. 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=