题目内容
如图,已知反比例函数 的图象经过点
的图象经过点 ,过点A作AB⊥x轴
,过点A作AB⊥x轴 于点B,且△AOB的面积为
于点B,且△AOB的面积为 .
.
(1)求k和m的值;
(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点C,求|AO|:|AC|的值;
(3)若D为坐标轴上一点,使△AOD是以AO为一腰的等腰三角形,请写出所有满足条件的D点的坐标.
解:(1)∵AB⊥x轴,
∴ .
.
∵k<0,
∴ .
.
∵ ,
,
∴m=2.
故k和m的值分别为 .
.
(2)由(1)得m=2,
∴ ,
,
∴由已知得 ,
,
∴ ,
,
∴一次函数为 ,令
,令 ,
,
∴ ,
,
∴ .
.
∵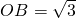 ,
,
∴ .
.
又∵AO= =
=
故 .
.
(3)由(2)知,AO= ,
,
又∵D为坐标轴上一点,使△AOD是以AO为一腰的等腰三角形,
∴由分析可知:
满足D点的坐标为:(0,± ),(0,4),(-2
),(0,4),(-2 ,0),(±
,0),(± ,0).
,0).
分析:(1)由三角形面积和反比例函数经过的点可以求出k和m的值;
(2)由(1)的结果,可得出AO的长度,再由线段与坐标轴的交点求出直线方程,从而得出C点坐标,得出AC的值;
(3)根据等腰三角形的性质及点在坐标轴上进行分类讨论,得出正确的结果.
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.同时还加入了分类讨论的内容.
∴
 .
.∵k<0,
∴
 .
.∵
 ,
,∴m=2.
故k和m的值分别为
 .
.(2)由(1)得m=2,
∴
 ,
,∴由已知得
 ,
,∴
 ,
,∴一次函数为
 ,令
,令 ,
,∴
 ,
,∴
 .
.∵
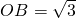 ,
,∴
 .
.又∵AO=
 =
=
故
 .
.(3)由(2)知,AO=
 ,
,又∵D为坐标轴上一点,使△AOD是以AO为一腰的等腰三角形,
∴由分析可知:
满足D点的坐标为:(0,±
 ),(0,4),(-2
),(0,4),(-2 ,0),(±
,0),(± ,0).
,0).分析:(1)由三角形面积和反比例函数经过的点可以求出k和m的值;
(2)由(1)的结果,可得出AO的长度,再由线段与坐标轴的交点求出直线方程,从而得出C点坐标,得出AC的值;
(3)根据等腰三角形的性质及点在坐标轴上进行分类讨论,得出正确的结果.
点评:本题综合考查反比例函数与方程组的相关知识点.先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.同时还加入了分类讨论的内容.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=