题目内容
k取何值时,关于x的一元二次方程x2+4kx+(2k-1)2=0有两个实数根并求出这时方程的根(用含k的代数式表示).
解:∵a=1,b=4k,c=(2k-1)2,
∴△=(4k)2-4(2k-1)2=16k-4.
当16k-4≥0,即k≥ 时,方程有两个实数根.
时,方程有两个实数根.
这时,方程的根是
x=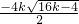 ,
,
即x1=-2k+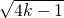 ,x2=-2k-
,x2=-2k-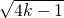 .
.
分析:一元二次方程有两个实数根,必须满足根的判别式△=b2-4ac≥0,从而求出k的取值范围,进而求出这时方程的根.
点评:本题考查了一元二次方程的根的判别式与根的关系和求根公式:x= (a≠0,b2-4ac≥0).
(a≠0,b2-4ac≥0).
∴△=(4k)2-4(2k-1)2=16k-4.
当16k-4≥0,即k≥
 时,方程有两个实数根.
时,方程有两个实数根.这时,方程的根是
x=
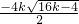 ,
,即x1=-2k+
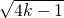 ,x2=-2k-
,x2=-2k-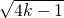 .
.分析:一元二次方程有两个实数根,必须满足根的判别式△=b2-4ac≥0,从而求出k的取值范围,进而求出这时方程的根.
点评:本题考查了一元二次方程的根的判别式与根的关系和求根公式:x=
 (a≠0,b2-4ac≥0).
(a≠0,b2-4ac≥0). 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目