题目内容
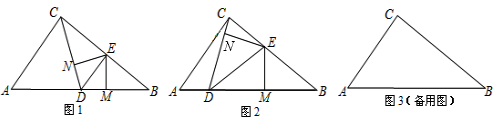
如图1,在Rt△ABC中,∠A=90°,AB=AC,BC=4 ,另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
,另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
(1)填空:GF的长度为______,等腰梯形DEFG的面积为______.
(2)操作:固定△ABC,将等腰梯形DEFG以每秒1个单位的速度沿BC方向向右运动,直到点D与点C重合时停止.设运动时间为x秒,运动后的等腰梯形为DEF’G’(如图2)
探究:在运动过程中,四边形BDG’G能否为菱形?若能,请求出此时x的值;若不能,请说明理由.

 解:(1)∵G、F分别是AB、AC的中点,
解:(1)∵G、F分别是AB、AC的中点,∴GF=
 BC=
BC= ×4
×4 =2
=2 ,
,过G点作GM⊥BC于M,
∵AB=AC,∠BAC=90°,BC=4
 ,G为AB中点
,G为AB中点∴GM=

∴S梯形DEFG=
 (2
(2 +4
+4 )×
)× =6,
=6,∴等腰梯形DEFG的面积为6
故答案为:2
 ,6;
,6;
(2)能为菱形
由BG∥DG′,GG′∥BC
∴四边形BDG′G是平行四边形
又AB=AC,∠BAC=90°,BC=4
 ,
,∴AB=AC=4,
当BD=BG=
 AB=2时,四边形BDG′G为菱形
AB=2时,四边形BDG′G为菱形此时可求得x=2,
∴当x=2秒时,四边形BDG′G为菱形
分析:(1)根据三角形中位线定理求出GF的长,再利用辅助线的帮助过点GM⊥BC于M.推出2GF=BC,G为AB中点可知GM的值.从而求出梯形面积.
(2)①BG∥DG′,GG′∥BC推出四边形BDG′G是平行四边形;当BD=BG=
 AB=2时,四边形BDG′G为菱形.
AB=2时,四边形BDG′G为菱形.点评:此题主要考查勾股定理、三角形中位线、等腰梯形的性质及菱形性质等知识点的综合运用,要求学生对所学知识能灵活运用.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目