��Ŀ����
����Ŀ����֪������y=x2+bx+c����A����1��0����B��3��0�����㣬��y���ཻ�ڵ�C���������ߵĶ���Ϊ��D
��1����������ߵĽ���ʽ����D�����ꡣ
��2������AC��CD��BD��BC�����AOC����BOC����BCD������ֱ�ΪS1 �� S2��S3 �� �õ�ʽ��ʾS1 �� S2 �� S3֮���������ϵ����˵������
��3��������ڣ����M������Ϊ��m��0������ʾ��MA�ij�������MN��BC���õ�����ʽ���AN�����ݡ�AMN�ס�ACM���õ�����ʽ���m���õ���M�����꣬���BC�Ľ���ʽ������MN��BC����ֱ��MN�Ľ���ʽ����⼴��
���𰸡�
��1��
�⣺��������y=x2+bx+c����A����1��0����B��3��0�����㣬
��![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪ��y=x2��2x��3��
y=x2��2x��3=��x��1��2��4��
���D����������1����4��
��2��
�⣺S1+S3=S2��
����D��DE��x���ڵ�E��DF��y����F��
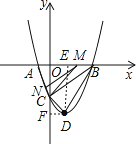
������ã�CD=![]() ��BD=
��BD=![]() ��BC=
��BC=![]() ��
��
CD2+BC2=BD2��
���BCD��ֱ�������Σ�
S1=![]() ��OA��OC=
��OA��OC=![]() ��
��
S2=![]() ��OB��OC=
��OB��OC=![]()
S3=![]() ��CD��BC=3��
��CD��BC=3��
��S1+S3=S2
��3��
�⣺���ڵ�Mʹ��AMN=��ACM��
���M��������m��0����
�ߩ�1��m��3��
��MA=m+1��AC=![]() ��
��
��MN��BC��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��ã�AN=![]() ��m+1����
��m+1����
�ߡ�AMN=��ACM����MAN=��CAM��
���AMN�ס�ACM��
��![]() =
=![]() ������m+1��2=
������m+1��2=![]()
![]() ��m+1����
��m+1����
��ã�m1=![]() ��m2=��1����ȥ����
��m2=��1����ȥ����
���M��������![]() ��0����
��0����
��BC�Ľ���ʽΪy=kx+b����B��3��0����C��0����3������ã�
![]() �����
�����![]() ��
��
��BC�Ľ���ʽΪy=x��3����MN��BC��
����ֱ��MN�Ľ���ʽΪy=x+b���ѵ�M������Ϊ��![]() ��0������ã�
��0������ã�
b=��![]() ��
��
��ֱ��MN�Ľ���ʽΪy=x��![]() ��
��
����������1�����ô���ϵ������������ߵĽ���ʽ�����䷽����һ��ʽ��Ϊ����ʽ�����D�����ꣻ
��2�����ݵ�����������AOC����BOC����������ù��ɶ������涨���жϡ�BCDΪֱ�������Σ��������������㼴�ɵõ��𰸣�
��3��������ڣ����M������Ϊ��m��0������ʾ��MA�ij�������MN��BC���õ�����ʽ���AN�����ݡ�AMN�ס�ACM���õ�����ʽ���m���õ���M�����꣬���BC�Ľ���ʽ������MN��BC����ֱ��MN�Ľ���ʽ����⼴�ɣ�
�����㾫����������Ĺؼ������������������ε����ʵ����֪ʶ�����ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�







