题目内容
【题目】平面直角坐标系xOy中，横坐标为a的点A在反比例函数y1＝
(x＞0)的图象上，点B与点A关于原点O对称，一次函数y2＝mx+n的图象经过点B.
(1)设a＝2，点C(4，2)在函数y1，y2的图象上.分别求函数y1，y2的表达式.
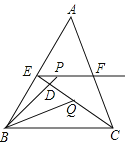
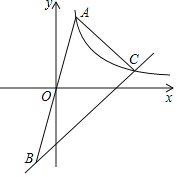
(2)如图，设函数y1，y2的图象相交于点C，点C的横坐标为3a，△ABC的面积为16，求k的值.
【答案】(1)y1＝
，y2＝x﹣2；(2)k＝6.
【解析】
(1)将点C(4，2)代入y1＝
，求出k的值，得到函数y1的表达式；把x＝a＝2代入y1＝，求出点A坐标，根据A和点A'关于原点对称，得到点A'的坐标，将点A'和点B的坐标代入y2＝mx+n，利用待定系数法求出函数y2的表达式；
(2)由反比例函数图象上点的坐标特征可得点A坐标，根据A和点B关于原点对称，得到点B(﹣a，﹣
).又点B在y2＝mx+n的图象上，那么点B(﹣a，﹣am+n).解方程即可得到结论.
解：(1)∵点C(4，2)在函数y1＝(x＞0)的图象上，
∴k＝4×2＝8，
∴函数y1的表达式为y1＝.
∵点A在y1＝的图象上，
∴x＝a＝2，y＝4，
∴点A(2，4).
∵A和点B关于原点对称，
∴点B的坐标为(﹣2，﹣4).
∵一次函数y2＝mx+n的图象经过点A'和点B，
∴
，
解之，得：
，
∴函数y2的表达式为y2＝x﹣2；
(2)∵点A的横坐标为a，
∴点A(a，).
∵A和点B关于原点对称，
∴点B的坐标为(﹣a，﹣).
∵点B在y2＝mx+n的图象上，
∴点B的坐标为(﹣a，﹣am+n).
∴﹣＝﹣am+n，
a2m＝an+k①.
∵点C的横坐标为3a，
∴点C(3a，3am+n)或(3a，
)，
∴3am+n＝，即9a2m+3an＝k②
由①②得：a2m＝
，an＝﹣
.
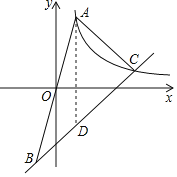
过点A作AD⊥x轴，交BC于点D，则点D(a，am+n)，
∴AD＝﹣am﹣n.
∵S△ABc＝
AD(xc﹣xb)＝4a(﹣am﹣n)＝16，
∴k﹣a2m﹣an＝8，
∴k﹣﹣(﹣)＝8，
∴k＝6.
