题目内容
若实数a,b,c两两不等,平面直角坐标系内有三点A(a+b,c),B(b+c,a),C(c+a,b),则这三点的位置关系是
- A.锐角三角形的三个顶点
- B.直角三角形的三个顶点
- C.钝角三角形的三个顶点
- D.三点共线
D
分析:利用待定系数法求出函数解析式,再将第三点代入即可判断.
解答:设函数解析式为y=kx+m,
将点A(a+b,c)和B(b+c,a)分别代入解析式得,
 ,
,
②-①得(c-a)k=a-c,
k=-1,
将k=-1代入①得,m=c+a+b,
函数解析式为y=-x+a+b+c,
将C(c+a,b)代入y=-x+a+b+c得,b=b,
可见,三点共线.
故选D.
点评:本题考查了一次函数图象上点的坐标特征,求出函数解析式是解题的关键.
分析:利用待定系数法求出函数解析式,再将第三点代入即可判断.
解答:设函数解析式为y=kx+m,
将点A(a+b,c)和B(b+c,a)分别代入解析式得,
 ,
,②-①得(c-a)k=a-c,
k=-1,
将k=-1代入①得,m=c+a+b,
函数解析式为y=-x+a+b+c,
将C(c+a,b)代入y=-x+a+b+c得,b=b,
可见,三点共线.
故选D.
点评:本题考查了一次函数图象上点的坐标特征,求出函数解析式是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;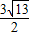 ?若存在求出P点坐标,若不存在请说明理由.
?若存在求出P点坐标,若不存在请说明理由. 时,求出此二次函数的解析式;
时,求出此二次函数的解析式; ?若存在求出P点坐标,若不存在请说明理由.
?若存在求出P点坐标,若不存在请说明理由.