题目内容
 如图,⊙O为△ABC的外接圆,BC=6,sin∠A=
如图,⊙O为△ABC的外接圆,BC=6,sin∠A=| 3 |
| 5 |
考点:圆周角定理,解直角三角形
专题:计算题
分析:过点B作直径BE,连结CE,如图,根据圆周角定理得到∠BCE=90°,∠E=∠A,则sin∠E=
,在Rt△BCE中理由正弦的定义可计算出BE=10,则OB=5.
| 3 |
| 5 |
解答:解:过点B作直径BE,连结CE,如图,
∵BE为直径,
∴∠BCE=90°,
∵∠E=∠A,
∴sin∠E=
,
在Rt△BCE中,sin∠E=
=
,
而BC=6,
∴BE=10,
∴OB=5,
即⊙O的半径为5.

∵BE为直径,
∴∠BCE=90°,
∵∠E=∠A,
∴sin∠E=
| 3 |
| 5 |
在Rt△BCE中,sin∠E=
| BC |
| BE |
| 3 |
| 5 |
而BC=6,
∴BE=10,
∴OB=5,
即⊙O的半径为5.
点评:本题考查了周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x=2,y=-1是方程ax+y=3的一组解,则a的值( )
| A、1 | B、2 | C、-1 | D、-2 |
 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DE⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DE⊥AC,垂足为F. 如图所示,AB∥CD,∠A=∠F,∠D=∠E,求∠EOF的度数.
如图所示,AB∥CD,∠A=∠F,∠D=∠E,求∠EOF的度数.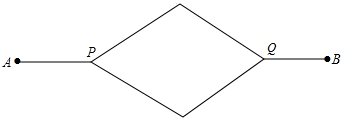 如图所示的道路,自A处出发通过P,Q到达B处,P,Q是三岔路口,假设当来到这些地点处就掷硬币,若出现正面就向右前进,若出现反面就向左前进,现若设掷硬币的次数是在四次以内,求到达B处的概率.
如图所示的道路,自A处出发通过P,Q到达B处,P,Q是三岔路口,假设当来到这些地点处就掷硬币,若出现正面就向右前进,若出现反面就向左前进,现若设掷硬币的次数是在四次以内,求到达B处的概率.