题目内容
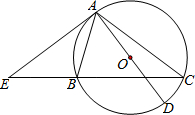 (2013•永州模拟)如图,△ABC内接于⊙O,AD是⊙O直径,E是CB延长线上一点,且∠BAE=∠C.
(2013•永州模拟)如图,△ABC内接于⊙O,AD是⊙O直径,E是CB延长线上一点,且∠BAE=∠C.(1)求证:直线AE是⊙O的切线;
(2)若EB=AB,cosE=
| 4 | 5 |
分析:(1)根据圆周角定理以及直径所对圆周角得出∠1+∠D=90°,进而得出∠DAE=90°,即可得出直线AE是⊙O的切线;
(2)根据锐角三角函数关系得出EB=
进而得出即可,再设BD=4k,则AD=5k.在Rt△ABD中,由勾股定理得:AB=3k,即可得出k的值,进而得出答案.
(2)根据锐角三角函数关系得出EB=
| EF |
| cosE |
解答: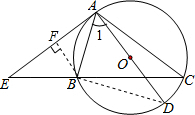 (1)证明:连接BD.
(1)证明:连接BD.
∵AD是⊙O的直径,
∴∠ABD=90°.
∴∠1+∠D=90°.
∵∠C=∠D,∠C=∠BAE,
∴∠D=∠BAE.
∴∠1+∠BAE=90°.
即∠DAE=90°.
∵AD是⊙O的直径,
∴直线AE是⊙O的切线.
(2)解:过点B作BF⊥AE于点F,则∠BFE=90°.
∵EB=AB,
∴∠E=∠BAE,EF=
AE=
×24=12.
∵∠BFE=90°,cosE=
,
∴EB=
=
×12=15.
∴AB=15.
由(1)∠D=∠BAE,又∠E=∠BAE,
∴∠D=∠E.
∵∠ABD=90°,
∴cosD=
=
.
设BD=4k,则AD=5k.
在Rt△ABD中,∠ABD=90°,由勾股定理得:
AB=
=3k,可求得k=5.
∴AD=25.
∴⊙O的半径为
.
 (1)证明:连接BD.
(1)证明:连接BD.∵AD是⊙O的直径,
∴∠ABD=90°.
∴∠1+∠D=90°.
∵∠C=∠D,∠C=∠BAE,
∴∠D=∠BAE.
∴∠1+∠BAE=90°.
即∠DAE=90°.
∵AD是⊙O的直径,
∴直线AE是⊙O的切线.
(2)解:过点B作BF⊥AE于点F,则∠BFE=90°.
∵EB=AB,
∴∠E=∠BAE,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BFE=90°,cosE=
| 4 |
| 5 |
∴EB=
| EF |
| cosE |
| 5 |
| 4 |
∴AB=15.
由(1)∠D=∠BAE,又∠E=∠BAE,
∴∠D=∠E.
∵∠ABD=90°,
∴cosD=
| BD |
| AD |
| 4 |
| 5 |
设BD=4k,则AD=5k.
在Rt△ABD中,∠ABD=90°,由勾股定理得:
AB=
| AD2-BD2 |
∴AD=25.
∴⊙O的半径为
| 25 |
| 2 |
点评:此题主要考查了圆的综合应用以及锐角三角形有关计算和圆周角定理等知识,根据已知得出BE=
是解题关键.
| EF |
| cosE |

练习册系列答案
相关题目
 (2013•永州模拟)下列如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )
(2013•永州模拟)下列如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )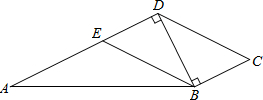 (2013•永州模拟)如图,在四边形ABCD中,∠ADB=∠CBD=90°,BE∥CD交AD于E,且EA=EB.若AB=4
(2013•永州模拟)如图,在四边形ABCD中,∠ADB=∠CBD=90°,BE∥CD交AD于E,且EA=EB.若AB=4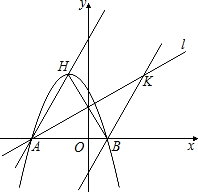 (2013•永州模拟)如图,抛物线y=mx2+2mx-3m(m≠0)的顶点为H,与x轴交于A、B两点(B点在A点右侧),点H、B关于直线l:
(2013•永州模拟)如图,抛物线y=mx2+2mx-3m(m≠0)的顶点为H,与x轴交于A、B两点(B点在A点右侧),点H、B关于直线l: