题目内容

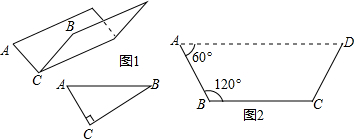
如图，横截面为等腰梯形的无盖水槽，其周长为40cm，底角∠ABC=∠DCB=60°．设AB为xcm，BC为ycm．
（1）求y与x的函数关系式并写出自变量的取值范围；
（2）当x为何值时，横截面的面积最大？最大面积是多少？

解：（1）过点A作AE⊥BC于点E，

∵四边形ABCD是等腰梯形，
∴AB=CD=x，
∵梯形的周长为40cm，
∴y+2x=40，
即可得：y=40-2x，
∵y＞x，
∴x＜ $\text{[math]}$ ，
故可得：y=40-2x（0＜x＜ $\text{[math]}$ ）．

（2）∵AD=BC-2BE=y-x，
∴S梯形ABCD= $\text{[math]}$ （AD+BC）×AE= $\text{[math]}$ （2y-x）× $\text{[math]}$ x=- $\text{[math]}$ $\text{[math]}$ （x-8）²+80 $\text{[math]}$ ，
当x=8时，S取得最大，最大面积为80 $\text{[math]}$ ．
分析：（1）过点A作AE⊥BC于点E，根据等腰梯形的性质即可得出y与x的函数关系式；
（2）表示出横截面积，运用配方法求最值即可．
点评：本题考查了等腰梯形的性质，解答本题的关键是作出辅助线，用x表示出各线段的长度，难度一般．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
（1）方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米²，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小；
（2）假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．

现有边长为180厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
某校九年级（2）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面，进行了如下探索：
（1）方案①：把它折成横截面为矩形的水槽，如图．
若∠ABC=90°，设BC=x厘米，该水槽的横截面面积为y厘米²，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽，如图．
若∠ABC=1 20°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．
（2）假如你是该兴趣小组中的成员，请你再提供一种方案，使你所设计的水槽的横截面

面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．

课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：
（1）方案①：把它折成横截面为直角三角形的水槽（如图1）．
若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米²，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽（如图2）．
若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小；
（2）假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．

现有边长为180厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．
某校九年级（2）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面，进行了如下探索：
（1）方案①：把它折成横截面为矩形的水槽，如图．
若∠ABC=90°，设BC=x厘米，该水槽的横截面面积为y厘米²，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？
方案②：把它折成横截面为等腰梯形的水槽，如图．
若∠ABC=1 20°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．
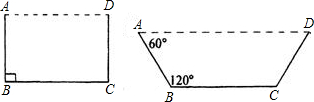（2）假如你是该兴趣小组中的成员，请你再提供一种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．