题目内容
18．从四张分别写有-2，-1，0，1的卡片中，随机抽取两张，将卡片的数字分别作为抛物线y=2（x-h）2+k的h和k值，求抛物线y=2（x-h）2+k的顶点在第三象限的概率．分析 抛物线y=2（x-h）2+k的顶点为（h，k），先列出图表，再根据第三象限内坐标的特点解答．列举出符合题意的各种情况的个数，再根据概率公式解答即可．
解答 解：列表如下：
| -2 | -1 | 0 | 1 | |
| -2 | （-2，-1） | （-2，0） | （-2，1） | |
| -1 | （-1，-2） | （-1，0） | （-1，1） | |
| 0 | （0，-2） | （0，-1） | （0，1） | |
| 1 | （1，-2） | （1，-1） | （1，0） |
∵抛物线y=2（x-h）2+k的顶点为（h，k），在第三象限，
∴符合条件的点为（-2，-1），（-1，-2），
∴P（顶点在第三象限）=$\frac{2}{9}$．
点评 此题考查利用列表法和树状图求概率，掌握概率是所求情况数与总情况数之比．第三象限点的符号，二次函数的顶点坐标是解决问题的关键．
练习册系列答案
相关题目
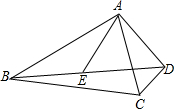如图，已知：∠ACB=∠ADE，∠ABC=∠AED，求证：△ABE∽△ACD．