题目内容
20．
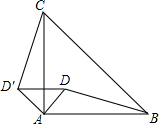如图，D是等腰直角△ABC内一点，BC是斜边，如果将△ABD绕点A逆时针方向旋转到△ACD 的位置（B与C重合，D与D′重合），则∠ADD′的度数是（ ）| A． | 25° | B． | 30° | C． | 35° | D． | 45° |
分析 先利用旋转的性质得到∠DAD′=∠BAC=90°，AD=AD′，则可判断△ADD′为等腰直角三角形，然后根据等腰直角三角形的性质求解．
解答 解：∵△ABC为等腰直角三角形，
∴∠BAC=90°，AB=AC，
∵△ABD绕点A逆时针方向旋转到△ACD 的位置（B与C重合，D与D′重合），
∴∠DAD′=∠BAC=90°，AD=AD′，
∴△ADD′为等腰直角三角形，
∴∠ADD′=45°．
故选D．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等腰直角三角形的判定与性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AD⊥AC，BC⊥AC，且AB=CD．求证：AB∥CD．
8．
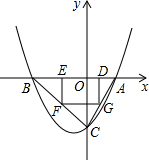如图，已知抛物线T：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线T上部分点的横坐标对应的纵坐标如下：
（1）写出A、B、C三点的坐标；
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
（3）当矩形DEFG的面积S取最大值m时
①抛物线T上是否存在点P，使S△PBC=m？若存在，请求出P点坐标；若不存在，请说明理由．
②连接DF并延长至点M，使FM=k•DF，若点M不在抛物线T上，求k的取值范围．
如图，已知抛物线T：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线T上部分点的横坐标对应的纵坐标如下：| x | … | -3 | -2 | 1 | 2 | … |
| y | … | -$\frac{5}{2}$ | -4 | -$\frac{5}{2}$ | 0 | … |
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
（3）当矩形DEFG的面积S取最大值m时
①抛物线T上是否存在点P，使S△PBC=m？若存在，请求出P点坐标；若不存在，请说明理由．
②连接DF并延长至点M，使FM=k•DF，若点M不在抛物线T上，求k的取值范围．
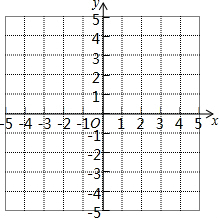如图是建有平面直角坐标系的正方形网格，请按下列要求操作：
的结果是（ ）
