题目内容
三角形ABC中，∠A=∠B，∠C=∠A+∠B，则这个三角形是 三角形．
考点：三角形内角和定理
专题：
分析：设∠A=∠B=x，则∠C=2x，再根据三角形内角和定理求出x的值，进而可得出结论．
解答：解：∵△ABC中，∠A=∠B，∠C=∠A+∠B，
∴设∠A=∠B=x，则∠C=2x，
∵∠A+∠B+∠C=180°，即x+x+2x=180°，解得x=45°，
∴∠C=2x=90°．
∴这个三角形是直角三角形．
故答案为：直角．
∴设∠A=∠B=x，则∠C=2x，
∵∠A+∠B+∠C=180°，即x+x+2x=180°，解得x=45°，
∴∠C=2x=90°．
∴这个三角形是直角三角形．
故答案为：直角．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
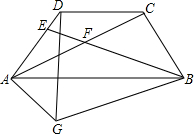如图，AB∥CD，∠ABC=∠BAD=60°，连接AC，点E在AD上，连接BE，使∠ABE=∠CAD，BE交AC于F，将△ABE沿AB翻折得△ABG，点E落在点G处，连接DG．若EF=
某市拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A，B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A，B，C的位置如图，请利用尺规作图找出音乐喷泉M的位置（要求：不写已知、求作、作法和结论，保留作图痕迹）；连结AM、CM，则AM