题目内容
 我市某校吴同学探究----“红灯绿灯时间差”的探讨----十字形的路口,东西、南北方向的行人车辆来来往往,车水马龙.为了不让双方挤在一起,红绿灯就应动而生,一个方向先过,另一个方向再过.
我市某校吴同学探究----“红灯绿灯时间差”的探讨----十字形的路口,东西、南北方向的行人车辆来来往往,车水马龙.为了不让双方挤在一起,红绿灯就应动而生,一个方向先过,另一个方向再过.在××路的十字路口,红灯绿灯的持续时间是不同的--红灯的时间总比绿灯长.即当东西方向红灯亮时,南北方向的绿灯要经过若干秒后才亮.这样方可确保十字路口的交通安全.
那么,如何根据实际情况设置红绿灯的时间差呢?
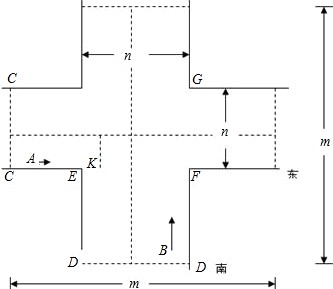
如图所示,假设十字路口是对称的,宽窄一致.设十字路口长为m米,宽为n米.当绿灯亮时最后一秒出来的骑车人A,不与另一方向绿灯亮时出来的机动车辆B相撞,即可保证交通安全.
根据调查自行车一般速度低于14km/h(即4m/s),机动车速度不超过28km/h(即8m/s).若红绿灯时间差为t秒.
通过上述数据,你能想出吴同学是怎样算出设置的时间差要满足t满足什么条件时,才能使车人不相撞.如××十字路口长约64米,宽约16米××路口实际时间差t=8s,做验证.
分析:本题中的不等式关系为:要想使A,B不相撞,那么A应该比B提前过FG线,由于A到K点南北方向的绿灯才亮,因此A从K到FG用的时间≤B从D1D2到FG用的时间.然后根据时间=路程÷速度,列出不等式,求得的自变量的取值范围中,最小的值就应该是设置的时间差.
解答:解:从C1C2线到FG线的距离=
+n=
骑车人A从C1C2线到K处时,另一方向绿灯亮,此时骑车人A前进距离=4t
K处到FG线距离=
-4t.
骑车人A从K处到达FG线所需的时间为
(
-4t)=
-t
D1D2线到EF线距离为(m-n)/2.
机动车B从D1D2线到EF线所需时间为
=
A通过FG线比B通过EF线要早一些方可避免碰撞事故.
∴
-t≤
,即t≥
即设置的时间差要满足t≥
时,才能使车人不相撞.
如××十字路口长约64米,宽约16米,理论上最少设置时间差为
=7秒,而实际设置时间差为8秒(8>7),符合要求.
| m-n |
| 2 |
| m+n |
| 2 |
骑车人A从C1C2线到K处时,另一方向绿灯亮,此时骑车人A前进距离=4t
K处到FG线距离=
| m+n |
| 2 |
骑车人A从K处到达FG线所需的时间为
| 1 |
| 4 |
| m+n |
| 2 |
| m+n |
| 8 |
D1D2线到EF线距离为(m-n)/2.
机动车B从D1D2线到EF线所需时间为
| 1 |
| 8 |
| m-n |
| 2 |
| m-n |
| 16 |
A通过FG线比B通过EF线要早一些方可避免碰撞事故.
∴
| m+n |
| 8 |
| m-n |
| 16 |
| m+3n |
| 16 |
即设置的时间差要满足t≥
| m+3n |
| 16 |
如××十字路口长约64米,宽约16米,理论上最少设置时间差为
| 64+16×3 |
| 16 |
点评:本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,理解车人不相撞的条件,列出不等式关系式即可求解.

练习册系列答案
相关题目