题目内容
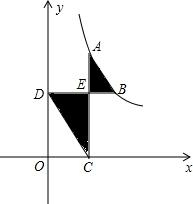 如图,AB=
如图,AB= ,线段AB的两端点在函数y=
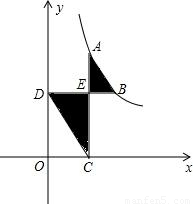
,线段AB的两端点在函数y=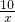 (x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于________.
(x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于________.
4
分析:首先假设出A,B点的坐标,进而得出AE= -2a,BE=
-2a,BE=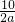 -a,再利用勾股定理求出a的值,进而得出阴影部分的面积.
-a,再利用勾股定理求出a的值,进而得出阴影部分的面积.
解答:如果设OC=a,则OD=2a,
点A、B坐标为A(a, ),B(
),B(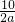 ,2a),
,2a),
∴AE= -2a,BE=
-2a,BE=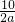 -a,
-a,
∵AB= ,
,
∴在Rt△AEB中,
AE2+BE2=AB2,
则( -2a)2+(
-2a)2+(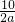 -a)2=(
-a)2=( )2,
)2,
整理得出:4a4-41a2+100=0,
解得:a2= 或a2=4,
或a2=4,
∴a=2.5或-2.5(不合题意舍去),
a=2或-2(不合题意舍去).
故A点坐标为:(2,5),B点坐标为:(2.5,4),
或A点坐标为:(2.5,4),B点坐标为:(2,5),
综上所述结合图形可得出A点坐标为:(2,5),B点坐标为:(2.5,4),
∴AE=1,BE=0.5,
∴DE=CO=2,
EC=4,
∴图中阴影部分的面积等于: ×DE×EC+
×DE×EC+ AE×BE=
AE×BE= ×2×4+
×2×4+ ×1×0.5=4
×1×0.5=4 .
.
故答案为:4 .
.
点评:本题考查的是反比例函数系数k的几何意义以及勾股定理,熟知在反比例函数y= 的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.
的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.

分析:首先假设出A,B点的坐标,进而得出AE=
 -2a,BE=
-2a,BE=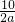 -a,再利用勾股定理求出a的值,进而得出阴影部分的面积.
-a,再利用勾股定理求出a的值,进而得出阴影部分的面积.解答:如果设OC=a,则OD=2a,
点A、B坐标为A(a,
 ),B(
),B(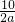 ,2a),
,2a),∴AE=
 -2a,BE=
-2a,BE=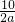 -a,
-a,∵AB=
 ,
,∴在Rt△AEB中,
AE2+BE2=AB2,
则(
 -2a)2+(
-2a)2+(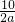 -a)2=(
-a)2=( )2,
)2,整理得出:4a4-41a2+100=0,

解得:a2=
 或a2=4,
或a2=4,∴a=2.5或-2.5(不合题意舍去),
a=2或-2(不合题意舍去).
故A点坐标为:(2,5),B点坐标为:(2.5,4),
或A点坐标为:(2.5,4),B点坐标为:(2,5),
综上所述结合图形可得出A点坐标为:(2,5),B点坐标为:(2.5,4),
∴AE=1,BE=0.5,
∴DE=CO=2,
EC=4,
∴图中阴影部分的面积等于:
 ×DE×EC+
×DE×EC+ AE×BE=
AE×BE= ×2×4+
×2×4+ ×1×0.5=4
×1×0.5=4 .
.故答案为:4
 .
.点评:本题考查的是反比例函数系数k的几何意义以及勾股定理,熟知在反比例函数y=
 的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.
的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键. 
练习册系列答案
相关题目
 如图:AB是线段CD的垂直平分线,则图中全等三角形的对数有( )
如图:AB是线段CD的垂直平分线,则图中全等三角形的对数有( ) 如图:AB是线段CD的垂直平分线,则图中全等三角形的对数有
如图:AB是线段CD的垂直平分线,则图中全等三角形的对数有
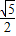 ,线段AB的两端点在函数y=
,线段AB的两端点在函数y=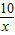 (x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于 .
(x>0)的图象上,AC⊥轴于点C,BD⊥y轴于点D,线段AC,BD相交于点E.当DO=2CO时,图中阴影部分的面积等于 .