题目内容
 如图,在4×4的方格纸中,每个方格边长为1,△ABC和△DEF都是格点三角形.
如图,在4×4的方格纸中,每个方格边长为1,△ABC和△DEF都是格点三角形.
(1)填空:∠ABC=________°,BC=________;
(2)判断△ABC与△DEF是否相似,并说明你的结论.
(1)解:由图可知:∠ABC=45°+90°=135°,
根据勾股定理:BC= =2
=2 ,
,
故答案为:135°,2 .
.
(2)解:△ABC∽△DEF,
理由是:AB=2,BC=2 ,∠ABC=135°,
,∠ABC=135°,
EF=2,
DE= =
= ,
,
∠DEF=90°+45°=135°=∠ABC,
∴ =
= ,
, =
= =
= ,
,
∴ =
= ,
,
∴△ABC∽△DEF.
分析:(1)根据图形求出∠ABC即可;根据勾股定理求出BC即可;
(2)求出EF、AB、DE的值,求出 和
和 的值,根据相似三角形的判定证出即可.
的值,根据相似三角形的判定证出即可.
点评:本题考查了相似三角形的判定,勾股定理等知识点的应用,关键是求出各个线段的长度,根据相似三角形的判定定理:有两边对应成比例,且夹角相等的两三角形相似,题型较好.
根据勾股定理:BC=
 =2
=2 ,
,故答案为:135°,2
 .
.(2)解:△ABC∽△DEF,
理由是:AB=2,BC=2
 ,∠ABC=135°,
,∠ABC=135°,EF=2,
DE=
 =
= ,
,∠DEF=90°+45°=135°=∠ABC,
∴
 =
= ,
, =
= =
= ,
,∴
 =
= ,
,∴△ABC∽△DEF.
分析:(1)根据图形求出∠ABC即可;根据勾股定理求出BC即可;
(2)求出EF、AB、DE的值,求出
 和
和 的值,根据相似三角形的判定证出即可.
的值,根据相似三角形的判定证出即可.点评:本题考查了相似三角形的判定,勾股定理等知识点的应用,关键是求出各个线段的长度,根据相似三角形的判定定理:有两边对应成比例,且夹角相等的两三角形相似,题型较好.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 3、如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )
3、如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )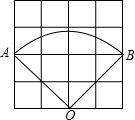 ,则扇形OAB周长等于
,则扇形OAB周长等于 如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移几个单位长度后与⊙B内切( )
如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移几个单位长度后与⊙B内切( ) 如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为l,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )
如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为l,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( ) 如图,在10*10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上),在给出的方格纸上,画出四边形ABCD关于直线L的对称的四边形A1B1C1D1.
如图,在10*10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上),在给出的方格纸上,画出四边形ABCD关于直线L的对称的四边形A1B1C1D1.