题目内容
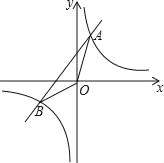
如图，已知反比例函数y1＝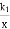
与一次函数y2＝k2x+b的图象交于点A（1，8），B（﹣4，m）两点．
（1）求k1，k2，b的值；
（2）求△AOB的面积；
（3）请直接写出不等式≤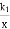
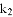x+b的解．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
津桥教育计算小状元系列答案题目内容
如图，已知反比例函数y1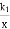＝与一次函数y2＝k2x+b的图象交于点A（1，8），B（﹣4，m）两点．
（1）求k1，k2，b的值；
（2）求△AOB的面积；
（3）请直接写出不等式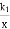≤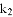x+b的解．
津桥教育计算小状元系列答案
与最简二次根式5
是同类二次根式，则a=_____．
，点P为对角线BD上一动点，点E在射线BC上，
C. 16
D. 8
B. 
C. 
D. 
