Question

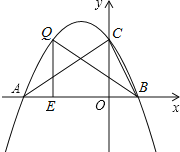
【题目】如图,抛物线y=ax2+bx向上平移2个单位之后,正好与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.

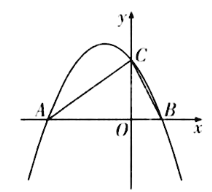
(1)求平移后抛物线的表达式;

(2)点Q是直线AC上方的抛物线上一点,过点Q作QE垂直于x轴,若以点B、Q、E为顶点的角形与△AOC相似,请求出Q点的坐标.

Answer 1

【答案】（1）；（2）Q（－2，2）或

【解析】

（1）利用待定系数法求函数解析式；（2）如图所示，若以点B、Q、E为顶点的三角形与△AOC相似，有两种情况，需要分类讨论，不要漏解；

解：（1）∵抛物线y=ax2+bx向上平移2个单位

∴抛物线y=ax2+bx+2

又∵抛物线过点A（-3，0），B（1，0），

∴，

解得： ，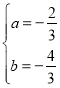

∴二次函数的关系解析式为

（2）如图所示，过点Q作QE垂直于x轴,设E（n，0），则BE=1-n，QE=

假设以点B、Q、E为顶点的三角形与△AOC相似，则有两种情况：

若△AOC∽△BEQ，则有： ，

即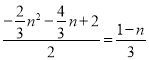 ，化简得：n2+n-2=0，
解得n1=-2，n2=1（与B重合，舍去），

∴n=-2，QE==2

∴Q（-2，2）；

若△AOC∽△BQE，则有：

即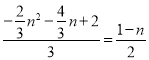，化简得：4n2-n-3=0，

解得n1=，n2=1（与B重合，舍去），

∴n=，QE=．

∴Q．
综上所述，存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似．
Q点坐标为（-2，2）或