题目内容

在Rt△ABC，AB=AC=2，∠BAC=90°，能完全覆盖住此三角形的最小圆的面积是（　　）
A、πB、2πC、3πD、4π
分析：由已知可得能完全覆盖住此三角形的最小圆为三角形的外接圆（如图），又∠BAC=90°，可知斜边AB为直径，先求AB，再求半径，计算圆的面积．
解答：精英家教网解：如图，∵∠C=90°，
∴能完全覆盖住△ABC的最小圆为以AB为直径的圆，
由勾股定理，得AB=
AC2+BC2
=2
2
，
∴圆的半径为
2
，面积为：π（
2
）2=2π．
故选B．
点评：本题考查了三角形的外接圆、直角三角形的性质和勾股定理等知识的综合应用．
练习册系列答案
相关题目
27、如图，已知在Rt△ABC，AB=AC，∠BAC=90°，AN是过点A的任一条直线，BD上AN于D，CE⊥AN于E．
（1）求证：DE=BD-CE；
（2）如将直线AN绕A点沿顺时针方向旋转，使它不经过△ABC的内部，再作BD⊥AN于D，CE⊥AN于E，那么DE、DB、CE之间还存在等量关系吗？如存在，请证明你的结论．

(本题满分7分)如图，已知在Rt△ABC，AB＝AC，∠BAC＝90°，过A的任一条直线AN，BD⊥AN于D，CE⊥AN于E。
⑴求证：DE＝BD－CE
⑵如将直线AN绕A点沿顺时针方向旋转，使它不经过△ABC的内部，再作BD⊥AN于D，CE⊥AN于E，那么DE、DB、CE之间存在等量关系吗？若存在，请证明你的结论？

(本题满分7分)如图，已知在Rt△ABC，AB＝AC，∠BAC＝90°，过A的任一条直线AN，BD⊥AN于D，CE⊥AN于E。

⑴求证：DE＝BD－CE

⑵如将直线AN绕A点沿顺时针方向旋转，使它不经过△ABC的内部，再作BD⊥AN于D，CE⊥AN于E，那么DE、DB、CE之间存在等量关系吗？若存在，请证明你的结论？

 

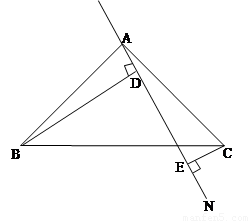
如图，已知在Rt△ABC，AB=AC，∠BAC=90°，AN是过点A的任一条直线，BD⊥AN于D，CE⊥AN于E．
（1）求证：DE=BD-CE；
（2）如将直线AN绕A点沿顺时针方向旋转，使它不经过△ABC的内部，再作BD⊥AN于D，CE⊥AN于E，那么DE、DB、CE之间还存在等量关系吗？如存在，请证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网