题目内容
在Rt△ACB中,∠ACB=90°,AC=8,AB=10,点O是斜边AB上的一个动点,过点O 作OD∥BC,交AC于点D,在线段OB上取一点E,使OE=OD,过点E作EF⊥ED,交射线AC于点F,交射线BC于点G.
(1)如图(1),求证:△ADE∽△AEF;
(2)设OA=x,AF=y,求y关于x的函数解析式,并写出它的定义域;
(3)当CG=2时,求线段AF的长.
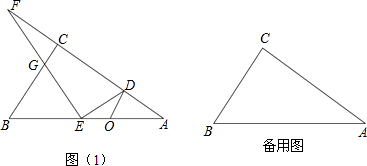
(1)证明:∵OD=OE∴∠ODE=∠OED
∵OD∥BC∴∠ODA=∠ACB
∵∠ACB=90°∴∠ODA=90°
∵EF⊥ED∴∠FED=90°
∴∠ADE=∠AEF
∵∠A=∠A∴△ADE∽△AEF
(2)解:在Rt△ACB中,∠ACB=90°,AC=8,AB=10
∴BC=6
∵OD∥BC∴
∵AO=x∴AD= ,OD=
,OD=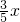
∵OD=OE∴OE=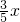
∴AE=
∵△ADE∽△AEF
∴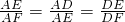
∴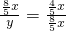
∴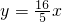
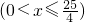
(3)解:当点G在线段BC上,图1:
∵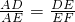 ,AE=
,AE= ,AD=
,AD=
∴EF=2DE
∵∠FED=90°∠GCF=90°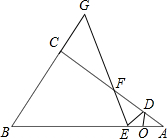
∴∠FED=∠GCF
∵∠F=∠F
∴△FED∽△FCG
∴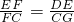
∵CG=2∴FC=4
∴AF=4+8=12
当点G在边BC的延长线上,(备用图)
同理可求得FC=4
∴AF=8-4=4
∴当CG=2时,线段AF的长为12或4.
分析:(1)首先利用等腰三角形的性质和平行线的性质可以得到∠ADE=∠AEF,而∠A=∠A,由此即可证明△ADE∽△AEF;
(2)首先利用勾股定理求出BC,然后利用平行线分线段成比例得到 ,接着由AO=x得到AD=
,接着由AO=x得到AD= ,OD=
,OD=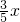 ,由OD=OE的OE=
,由OD=OE的OE=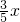 ,所以AE=
,所以AE= ,最后利用(1)的结论和相似三角形的性质即可解决问题;
,最后利用(1)的结论和相似三角形的性质即可解决问题;
(3)有两种情况:
①当点G在线段BC上,如图1,由(1)得到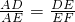 ,AE=
,AE= ,AD=
,AD= ,接着得到EF=2DE,然后利用已知条件可以证明△FED∽△FCG,最后利用相似三角形的性质即可求出FC=4,也就求出AF;
,接着得到EF=2DE,然后利用已知条件可以证明△FED∽△FCG,最后利用相似三角形的性质即可求出FC=4,也就求出AF;
②当点G在边BC的延长线上,(备用图).方法和①一样求出CG,然后求出AF.
点评:此题主要考查了相似三角形的性质与判定,也考查了勾股定理及求函数解析式,综合性比较强,解题的关键是多次利用相似三角形的性质与判定解决问题.
∵OD∥BC∴∠ODA=∠ACB
∵∠ACB=90°∴∠ODA=90°
∵EF⊥ED∴∠FED=90°
∴∠ADE=∠AEF
∵∠A=∠A∴△ADE∽△AEF
(2)解:在Rt△ACB中,∠ACB=90°,AC=8,AB=10
∴BC=6
∵OD∥BC∴

∵AO=x∴AD=
 ,OD=
,OD=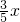
∵OD=OE∴OE=
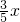
∴AE=

∵△ADE∽△AEF
∴
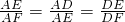
∴
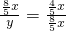
∴
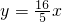
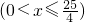
(3)解:当点G在线段BC上,图1:
∵
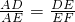 ,AE=
,AE= ,AD=
,AD=
∴EF=2DE
∵∠FED=90°∠GCF=90°

∴∠FED=∠GCF
∵∠F=∠F
∴△FED∽△FCG
∴
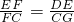
∵CG=2∴FC=4
∴AF=4+8=12
当点G在边BC的延长线上,(备用图)
同理可求得FC=4
∴AF=8-4=4
∴当CG=2时,线段AF的长为12或4.
分析:(1)首先利用等腰三角形的性质和平行线的性质可以得到∠ADE=∠AEF,而∠A=∠A,由此即可证明△ADE∽△AEF;
(2)首先利用勾股定理求出BC,然后利用平行线分线段成比例得到
 ,接着由AO=x得到AD=
,接着由AO=x得到AD= ,OD=
,OD=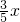 ,由OD=OE的OE=
,由OD=OE的OE=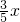 ,所以AE=
,所以AE= ,最后利用(1)的结论和相似三角形的性质即可解决问题;
,最后利用(1)的结论和相似三角形的性质即可解决问题;(3)有两种情况:
①当点G在线段BC上,如图1,由(1)得到
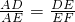 ,AE=
,AE= ,AD=
,AD= ,接着得到EF=2DE,然后利用已知条件可以证明△FED∽△FCG,最后利用相似三角形的性质即可求出FC=4,也就求出AF;
,接着得到EF=2DE,然后利用已知条件可以证明△FED∽△FCG,最后利用相似三角形的性质即可求出FC=4,也就求出AF;②当点G在边BC的延长线上,(备用图).方法和①一样求出CG,然后求出AF.
点评:此题主要考查了相似三角形的性质与判定,也考查了勾股定理及求函数解析式,综合性比较强,解题的关键是多次利用相似三角形的性质与判定解决问题.

练习册系列答案
相关题目
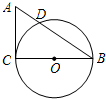 在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D. (2013•湖州)如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则cosB的值为
(2013•湖州)如图,已知在Rt△ACB中,∠C=90°,AB=13,AC=12,则cosB的值为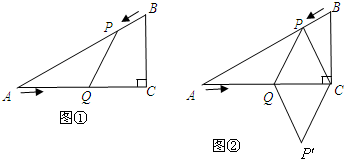
 (2013•丹东一模)在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
(2013•丹东一模)在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )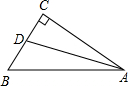 如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )
如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )