题目内容
已知关于x的方程|x|=ax-a有正根且没有负根，求a的取值范围．
解：当x≥0时，
x=ax-a，
∴x=
．
当x＜0时，
-x=ax-a，解得x=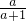
，
∵解为非负值，
∴
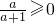或a=-1．
∴
，
∴
，
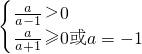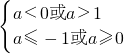综合可得，a＞1或a≤-1．
分析：根据绝对值的性质和方程|x|=ax-a有正根且没有负根，确定a的取值范围．
点评：根据绝对值的性质，要分x≥0和x＜0，两种情况进行讨论，确定a的取值范围．
x=ax-a，
∴x=
．当x＜0时，
-x=ax-a，解得x=
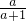，∵解为非负值，
∴
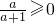或a=-1．∴
，∴
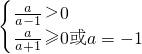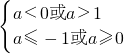，综合可得，a＞1或a≤-1．
分析：根据绝对值的性质和方程|x|=ax-a有正根且没有负根，确定a的取值范围．
点评：根据绝对值的性质，要分x≥0和x＜0，两种情况进行讨论，确定a的取值范围．
练习册系列答案
相关题目