题目内容
甲、乙、丙三人一起进行百米赛跑(假定三人均为匀速直线运动).如果当甲到达终点时,乙距终点还有5米,丙距终点还有10米,那么当乙到达终点时,丙距终点还有分析:易得乙丙两人的速度比为95:90,等量关系为:乙跑5米用的时间=丙跑[10-(乙到达终点时,丙距终点的距离)]所用时间,把相关数值代入求解即可.
解答:解:∵当甲到达终点时,乙距终点还有5米,丙距终点还有10米,
∴乙跑了95米,丙跑了90米,
∴设乙的速度为95a米/秒,丙的速度为90a米/秒,当乙到达终点时,丙距终点还有x米.
=
,
解得x=5
.
故答案为:5
.
∴乙跑了95米,丙跑了90米,
∴设乙的速度为95a米/秒,丙的速度为90a米/秒,当乙到达终点时,丙距终点还有x米.
| 5 |
| 95a |
| 10-x |
| 90a |
解得x=5
| 5 |
| 19 |
故答案为:5
| 5 |
| 19 |
点评:考查一元一次方程的应用,根据两人跑的时间相等得到等量关系式解决本题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:
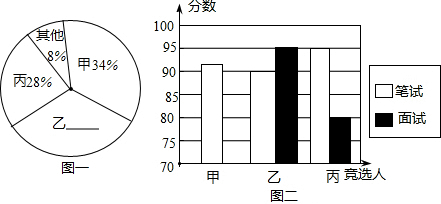
其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?