题目内容

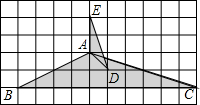精英家教网在边长为1的正方形网格中有A、B、C、D、E五个点，问△ABC与△ADE是否相似？为什么？由此，你还能找出图中相似的三角形吗？若能，请找出来，并说明理由．
分析：根据勾股定理分别计算AB、BC、AC、AE、AD、DE、CE、BD的长度，根据对应边比值相等的性质可以判定△ABC∽△ADE，△ABD∽△ACE即可解题．
解答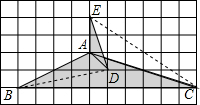：精英家教网解：AB=
22+42
=2
5
，BC=10，AC=
22+62
=2
10
，
AE=2，AD=
2
，DE=
12+32
=
10
，CE=
42+62
=2
13
，
BD=
12+52
=
26
，
∴
AB
AD
=
AC
AE
=
BC
DE
=
10
，
CE
BD
=
AC
AB
=
AE
AD
=
2
，
∴△ABC∽△ADE，△ABD∽△ACE．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比值相等的性质，考查了勾股定理在直角三角形中的运用，本题中根据勾股定理计算各边的长度是解题的关键．
练习册系列答案
相关题目
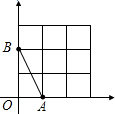精英家教网如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．
（1）求线段AB所在直线的函数解析式，并写出当0≤y≤2时，自变量x的取值范围；
（2）将线段AB绕点B逆时针旋转90°，得到线段BC，请在答题卡指定位置画出线段BC．若直线BC的函数解析式为y=kx+b，则y随x的增大而
 
（填“增大”或“减小”）．
如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．
（1）若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有
4
4
个．
（2）将线段AB沿x轴向右平移2格得线段CD，请你求出线段CD所在的直线函数解析式．
如图所示，在平面直角坐标系中，A、B、C、D均在边长为1的正方形网格格点上．
（1）求线段AB所在直线的解析式，并写出当0≤y≤2时，自变量x的取值范围；
（2）若把直线y=kx+b中的k叫做直线的斜率，那么直线AB和直线AD的斜率有什么关系？直线AB和直线CD的斜率有什么关系？

如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．

1.求线段AB所在直线的函数关系式，并写出当0≤y≤2时，自变量x的取值范围；

2.将线段AB绕点B逆时针旋转90°，得到线段BC，若直线BC的函数关系式为y=kx+b，则y随x的增大而      （填“增大”或“减小”）．

 

 

 

 

 

 

如图8,在平面直角坐标系中,、均在边长为1的正方形网格格点上.

(1)求线段所在直线的函数解析式,并写出当时,自变量的取值范围；

(2)将线段绕点逆时针旋转,得到线段,请在指定位置画出线段.若直线的函数解析式为,则随的增大而             (填“增大”或“减小”).

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网