题目内容
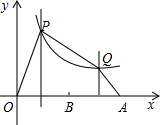 如图,A为x轴正半轴上一点,B为OA的中点,线段OB、AB的垂直平分线分别交双曲线y=
如图,A为x轴正半轴上一点,B为OA的中点,线段OB、AB的垂直平分线分别交双曲线y=| k | x |
2
2
.分析:首先设点B的横坐标为2a(a>0),由题意可求得点A,C,D,P,Q的坐标,又由S四边形OAQP=S△OPC+S四边形PCDQ+S△ADQ,即可得方程
k+
(
+
)×2a+
×
×a=4,继而求得k的值.
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 3a |
| k |
| a |
| 1 |
| 2 |
| k |
| 3a |
解答: 解:设点B的横坐标为2a(a>0),
解:设点B的横坐标为2a(a>0),
∵B为OA的中点,
∴点A的横坐标为4a,
∵线段OB、AB的垂直平分线分别交双曲线y=
(x>0)于P、Q两点,设与x轴的交点分别为C,D.
∴点P的横坐标为a,点Q的横坐标为3a,
∴点P的坐标为:(a,
),点Q的坐标为:(3a,
),
∵S四边形OAQP=4,
∴S四边形OAQP=S△OPC+S四边形PCDQ+S△ADQ=
k+
(
+
)×2a+
×
×a=4,
∴2k=4,
解得:k=2.
故答案为:2.
 解:设点B的横坐标为2a(a>0),
解:设点B的横坐标为2a(a>0),∵B为OA的中点,
∴点A的横坐标为4a,
∵线段OB、AB的垂直平分线分别交双曲线y=
| k |
| x |
∴点P的横坐标为a,点Q的横坐标为3a,
∴点P的坐标为:(a,
| k |
| a |
| k |
| 3a |
∵S四边形OAQP=4,
∴S四边形OAQP=S△OPC+S四边形PCDQ+S△ADQ=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 3a |
| k |
| a |
| 1 |
| 2 |
| k |
| 3a |
∴2k=4,
解得:k=2.
故答案为:2.
点评:此题考查了反比例函数的几何意义、线段垂直平分线的性质以及四边形的面积问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 数
数
 与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.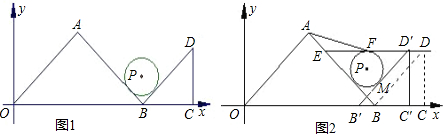
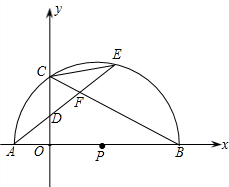
 (2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.
(2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.