题目内容
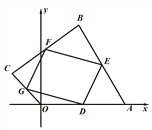
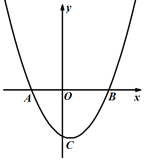
【题目】如图,抛物线![]() 分别交x轴于点A,B(点A在点B的左侧),交y轴于点C,D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′,B′D .
分别交x轴于点A,B(点A在点B的左侧),交y轴于点C,D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′,B′D .
(1)求点A,B的坐标.
(2)当点B′落坐标轴上时,求点D的坐标.
(3)在点D的运动过程中,△AB′D 的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
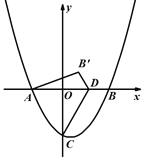
【答案】(1)A(-2,0) , B(3,0) (2)B’在以C为圆心,CB为半径的圆C上;(3)① ![]() ②(
②(![]() )③(
)③(![]() )
)
【解析】分析:(1)令y=0,可求得x的值,从而可确定A、B两点坐标;
(2)分两种情况进行讨论:①当B’点落在x轴上,②当B’点落在y轴上,利用对称性求解即可;
(3)如图,分三种情况进行求解.
详解(1)由y=0解得x1=-2,x2=3,
∴ A(-2,0) , B(3,0)
(2)B’在以C为圆心,CB为半径的圆C上;
①当B’点落在x轴上时,D(0,0);
②当B’点落在y轴上时,如图1,CB’=CB=![]() ,
,
∵∠OB’D=45°
∴OD=OB’=![]() -3
-3
∴ D(![]() )
)
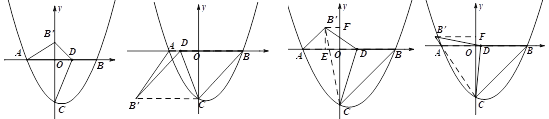
图1 图2 图3 图4
(3)①∠B’DA=45°时,如图1,OB’=![]() -3,B’(0,
-3,B’(0,![]() -3).
-3).
如图2,连接CB’,∠B’DA=∠CBD=45°,∴DB’∥BC,可得四边形DB’CB是菱形,B’(-![]() -3).
-3).
②∠B’AD=45°如图3,连接CB’,过点B’分别作坐标轴的垂线,垂足为E、F,设线段FB’的长为m,B’E=AE=2-m,可得CF=5-m,在直角三角形CFB’中,![]() ,解得
,解得![]() ,B’(
,B’(![]() ,
,![]() ).
).
③如图4,∠AB’D=45°,连接CB’,过点B’作Y轴的垂线,垂足为点F,由轴对称性质可得,∠CB’D=∠CBD=45°,所以当∠AB’D=45°时,点A在线段CB’上,所以![]() ,设线段FB’的长为2m,FC=3m,
,设线段FB’的长为2m,FC=3m,![]() ,解得:
,解得:![]() ,
,![]() .
.