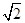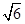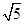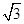题目内容
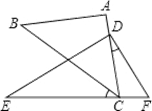
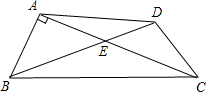
如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC=90°，∠CED=45°，∠DCE=30°，DE=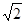
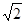，BE=2．求CD的长和四边形ABCD的面积．
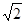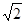，BE=2．求CD的长和四边形ABCD的面积．2 
解：过点D作DH⊥AC，
∵∠CED=45°，DH⊥EC，DE=，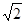
∴EH=DH，
∵EH2+DH2=ED2，
∴EH2=1，
∴EH=DH=1，
又∵∠DCE=30°，
∴DC=2，HC=
，
∵∠AEB=45°，∠BAC=90°，
BE=2，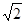
∴AB=AE=2，
∴AC=2+1+=3+，
∴S四边形ABCD=
×2×（3+）+×1×（3+）=．
利用等腰直角三角形的性质得出EH=DH=1，进而得出再利用直角三角形中30°所对边等于斜边的一半得出CD的长，求出AC，AB的长即可得出四边形ABCD的面积．
∵∠CED=45°，DH⊥EC，DE=
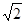，∴EH=DH，
∵EH2+DH2=ED2，
∴EH2=1，
∴EH=DH=1，
又∵∠DCE=30°，
∴DC=2，HC=
，∵∠AEB=45°，∠BAC=90°，
BE=2
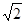，∴AB=AE=2，
∴AC=2+1+
=3+，∴S四边形ABCD=
×2×（3+）+×1×（3+）=．利用等腰直角三角形的性质得出EH=DH=1，进而得出再利用直角三角形中30°所对边等于斜边的一半得出CD的长，求出AC，AB的长即可得出四边形ABCD的面积．
练习册系列答案
名校课堂系列答案
相关题目
