题目内容
【题目】如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC= ![]() ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC= ![]() 中正确的有( )
中正确的有( )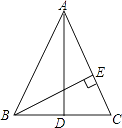
A.①②
B.②③
C.①②③
D.①②③④
【答案】A
【解析】解:∵AD⊥BC垂足为点D,AD是BC边上的中线,
∴AD垂直平分BC,
∴AB=AC,∴①正确;
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD= ![]() ∠BAC,
∠BAC,
∵BE⊥AC,AD⊥BC,
∴∠EBC+∠C=90°,∠DAC+∠C=90°,
∴∠EBC=∠DAC,
∴∠EBC= ![]() ∠BAC,∴②正确;
∠BAC,∴②正确;
∵AE2=AB2﹣BE2 , CE2=BC2﹣BE2 , AB≠BC,
∴AE≠CE,∴③错误;
∵∠BAC≠∠ABC,∠EBC= ![]() ∠BAC,
∠BAC,
∴∠EBC≠ ![]() ∠ABC,∴④错误;
∠ABC,∴④错误;
∴①②都正确;
故答案为:A.
由题知AD垂直平分BC,根据垂直平分线上的点到角两边的距离相等得出AB=AC ;根据等腰三角形的三线合一得出∠BAD=∠CAD= ![]() ∠BAC,然后又根据同角的余角相等得出∠EBC=∠DAC,通过等量代换得出∠EBC=
∠BAC,然后又根据同角的余角相等得出∠EBC=∠DAC,通过等量代换得出∠EBC= ![]() ∠BAC ;根据勾股定理得出AE2=AB2﹣BE2 , CE2=BC2﹣BE2 , 又AB≠BC,从而得出AE≠CE ;根据∠BAC≠∠ABC,∠EBC=
∠BAC ;根据勾股定理得出AE2=AB2﹣BE2 , CE2=BC2﹣BE2 , 又AB≠BC,从而得出AE≠CE ;根据∠BAC≠∠ABC,∠EBC= ![]() ∠BAC,从而得出∠EBC≠
∠BAC,从而得出∠EBC≠ ![]() ∠ABC 。
∠ABC 。

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目