题目内容
已知:∠AOB=40°,OC⊥OA,OD平分∠BOC,求∠AOD的度数.
考点:角平分线的定义
专题:
分析:分类讨论:OB在∠AOC的内部;OB在∠AOC的外部.根据垂直,可得所成的角是90°,根据角的和差,可得∠BOC的度数,根据角平分线,可得∠BOD的度数,再根据角的和差,可得答案.
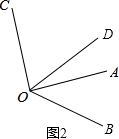
解答:解:符合题意的图形有两个,如图1、图2,
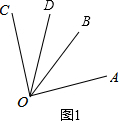 在图1中,OB在∠AOC的内部.
在图1中,OB在∠AOC的内部.
∵OC⊥OA,
∴∠AOC=90°.
∵∠AOB=40°,
∴∠BOC=∠AOC-∠AOB=50°.
∵OD平分∠BOC,
∴∠BOD=
∠BOC=25°,
 ∴∠AOD=∠AOB+∠BOD=65°;
∴∠AOD=∠AOB+∠BOD=65°;
在图2中,OB在∠AOC的外部.
∵OC⊥OA,
∴∠AOC=90°.
∵∠AOB=40°,
∴∠BOC=∠AOB+∠AOC=130°.
∵OD平分∠BOC,
∴∠BOD=
∠BOC=65°,
∴∠AOD=∠BOD-∠AOB=25°.
综上,∠AOD的度数为65°或25°.
 在图1中,OB在∠AOC的内部.
在图1中,OB在∠AOC的内部.∵OC⊥OA,
∴∠AOC=90°.
∵∠AOB=40°,
∴∠BOC=∠AOC-∠AOB=50°.
∵OD平分∠BOC,
∴∠BOD=
| 1 |
| 2 |
 ∴∠AOD=∠AOB+∠BOD=65°;
∴∠AOD=∠AOB+∠BOD=65°;在图2中,OB在∠AOC的外部.
∵OC⊥OA,
∴∠AOC=90°.
∵∠AOB=40°,
∴∠BOC=∠AOB+∠AOC=130°.
∵OD平分∠BOC,
∴∠BOD=
| 1 |
| 2 |
∴∠AOD=∠BOD-∠AOB=25°.
综上,∠AOD的度数为65°或25°.
点评:本题考查了垂直的定义,角平分线的定义,先求出∠BOC的度数,再求出∠BOD的度数,最后求出答案,有两种情况,以防漏掉.

练习册系列答案
相关题目
小刚做了一道数学题:“已知两个多项式为A,B,求A+B的值,”他误将“A+B”看成了“A-B”,结果求出的答案是x-y,若已知B=3x-2y,那么原来A+B的值应该是( )
| A、4x+3y | B、2x-y |
| C、-2x+y | D、7x-5y |
下列事件是随机事件的是( )
| A、明天太阳从东方升起 |
| B、任意画一个三角形,其内角和是360° |
| C、通常温度降到0℃以下,纯净的水结冰 |
| D、射击运动员射击一次,命中靶心 |
若3a=2b,则
的值为( )
| a-b |
| a |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
 如图,⊙O是△ABE的外接圆,点O在AB上,BF为⊙O的切线,∠ABE=30°,过点O作OD⊥BE,垂足为D,延长OD交BF于点C,求证:BE=BC.
如图,⊙O是△ABE的外接圆,点O在AB上,BF为⊙O的切线,∠ABE=30°,过点O作OD⊥BE,垂足为D,延长OD交BF于点C,求证:BE=BC.