Question

在Rt△ABC中，∠C=90°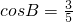，，把这个直角三角形绕顶点C旋转后得到Rt△A′B′C，其中点B′正好落在AB上，A′B′与AC相交于点D，那么=________．

Answer 1

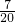
分析：作CH⊥AB于H，先在Rt△ABC中，根据余弦的定义得到cosB==，设BC=3x，则AB=4x，再根据勾股定理计算出AC=4x，在Rt△HBC中，根据余弦的定义可计算出BH=x，接着根据旋转的性质得CA′=CA=4x，CB′=CB，∠A′=∠A，所以根据等腰三角形的性质有B′H=BH=x，则AB′=x，然后证明△ADB′∽△A′DC，再利用相似比可计算出B′D与DC的比值．
解答：解：作CH⊥AB于H，如图，
在Rt△ABC中，∠C=90°，cosB==，设BC=3x，则AB=5x，
AC==4x，
在Rt△HBC中，cosB==，而BC=3x，
∴BH=x，
∵Rt△ABC绕顶点C旋转后得到Rt△A′B′C，其中点B′正好落在AB上，
∴CA′=CA=4x，CB′=CB，∠A′=∠A，
∵CH⊥BB′，
∴B′H=BH=x，
∴AB′=AB-B′H-BH=x，
∵∠ADB′=∠A′DC，∠A′=∠A，
∴△ADB′∽△A′DC，
∴=，即=，
∴=．
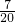故答案为．
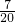点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了三角形相似的判定与性质以及锐角三角形函数．