Question

【题目】已知半径为1的⊙O中，弦AC=，弦AB=，则∠CAB的度数为（　　）

A. 15° B. 60° C. 75° D. 15°或75°

Answer 1

【答案】D

【解析】

先根据题意画出图形，分别作AC、AB的垂线，连接OA，再根据锐角三角函数的定义求出∠OAD及∠OAE的度数，即可得出结论．

有两种情况：

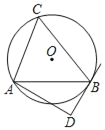
①如图1，当两弦AC、AB在圆心的两侧时，过O作OD⊥AB于点D，OE⊥AC于点E，连接OA，

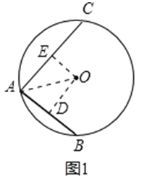
∵AB=,AC=，

∴AD=,AE=，

在Rt△AOD中，

∵cos∠OAD==，

∴∠OAD=45°，

在Rt△AOE中，

∵cos∠OAE==，

∴∠OAE=30°，

∴∠BAC=∠OAD+∠OAE=45°+30°=75°；

②如图2,当两弦AC、AB在圆心的同侧时，

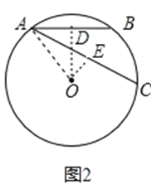
由①可知∠OAD=45°,∠OAE=30°，

∴∠BAC=∠OAD∠OAE=45°30°=15°；

综上所述，∠BAC的度数是75°或15°.

故选：D.